
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
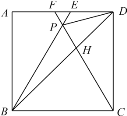
①△ABE≌△DCF;②∠PDF=15°;③![]() ;④
;④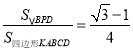 ,其中正确的结论有( )
,其中正确的结论有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①利用等边三角形的性质以及正方形的性质得出∠ABE=∠DCF=30°,再直接利用全等三角形的判定方法得出答案;
②利用等边三角形的性质结合正方形的性质得出∠CPD=75°,进而得出答案;
③先得出![]() ,再根据CD=BP得出
,再根据CD=BP得出![]() ,进而根据相似三角形的性质即得.
,进而根据相似三角形的性质即得.
;
④根据三角形面积计算公式,结合图形得到△BPD的面积=△BCP的面积+△CDP面积-△BCD的面积,得出答案.
解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
在△ABE与△CDF中,
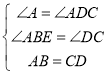 ,
,
∴△ABE≌△DCF,故①正确;
∵PC=BC=DC,∠PCD=30°,
∴∠CDP=75°,
∴∠PDF=∠ADC-∠CDP=90°-75°=15°,故②正确;
∵∠PCD=30°,
∴DF=![]() ,根据勾股定理CD=
,根据勾股定理CD=![]() FC,
FC,
∵∠DBC=45°,∠BCF=60°,
∵∠DBC=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴![]() ,故③正确;
,故③正确;
如图,过P作PM⊥CD,PN⊥BC,
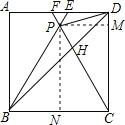
设正方形ABCD的边长是4,
∵△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°,
∴![]() ,
,
![]() ,
,
S△BPD=S四边形PBCD-S△BCD=S△PBC+S△PDC-S△BCD
![]()
![]()
![]()
![]() ,
,
∴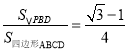 ,故④正确;
,故④正确;
故正确的有4个,
故选:D.


科目:初中数学 来源: 题型:
【题目】某城市绿化工程进行招标,现有甲、乙两个工程队投标,已知甲队单独完成这项工程需要60天.经测算:如果甲队先做20天,再由甲队、乙队合作12天,那么此时共完成总工作量的![]() .
.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款4.5万元,乙队施工一天需付工程款2万元,该工程由甲乙两队合作若干天后,再由乙队完成剩余的工作,若要求完成此项工程的工程款不超过186万元,求甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
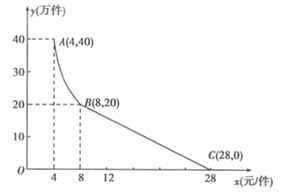
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
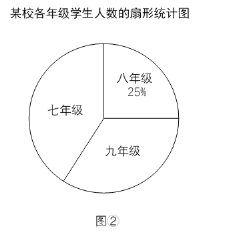
【题目】某校七、八、九年级共有1000名学生.学校统计了各年级学生的人数,绘制了图①、图②两幅不完整的统计图.
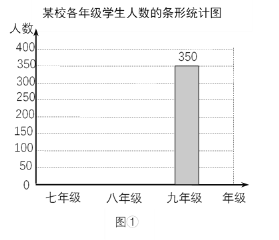
(1)将图①的条形统计图补充完整.
(2)图②中,表示七年级学生人数的扇形的圆心角度数为 °.
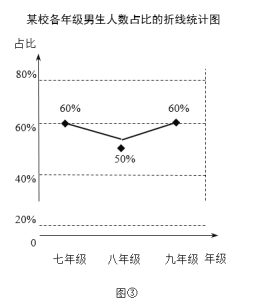
(3)学校数学兴趣小组调查了各年级男生的人数,绘制了如图③所示的各年级男生人数占比的折线统计图(年级男生人数占比=该年级男生人数÷该年级总人数×100%).请结合相关信息,绘制一幅适当的统计图,表示各年级男生及女生的人数,并在图中标明相应的数据.
查看答案和解析>>
科目:初中数学 来源: 题型:
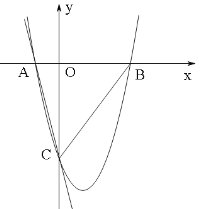
【题目】如图,一次函数y =﹣4x﹣4的图像与x轴、y轴分别交于A、C两点,抛物线y=![]() 的图像经过A、C两点,且与x轴交于点B.
的图像经过A、C两点,且与x轴交于点B.
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上找一点E,使点E到点A的距离与到点C的距离之和最小,求出此点E的坐标;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点![]() ,用测角仪测出看塔顶
,用测角仪测出看塔顶![]() 的仰角
的仰角![]() ,在
,在![]() 点和塔之间选择一点
点和塔之间选择一点![]() ,测出看塔顶
,测出看塔顶![]() 的仰角
的仰角![]() ,然后用皮尺量出
,然后用皮尺量出![]() .
.![]() 两点的距离为
两点的距离为![]() m,自身的高度为
m,自身的高度为![]() m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(![]() ,结果保留整数).
,结果保留整数).
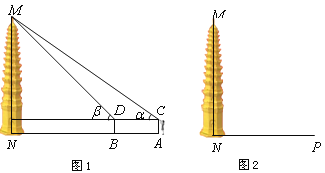
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影![]() 的长为
的长为![]() m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据? .
查看答案和解析>>
科目:初中数学 来源: 题型:
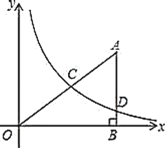
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直
垂直![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,与边
,与边![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)经过![]() 、
、![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com