
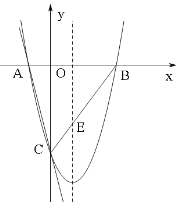
����Ŀ����ͼ��һ�κ���y =��4x��4��ͼ����x�ᡢy��ֱ���A��C���㣬������y=![]() ��ͼ��A��C���㣬����x�ύ�ڵ�B��
��ͼ��A��C���㣬����x�ύ�ڵ�B��
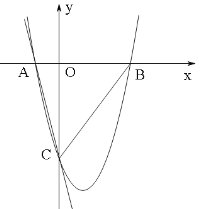
��1���������ߵĺ�������ʽ��
��2���������ߵĶԳ�������һ��E,ʹ��E����A�ľ����뵽��C�ľ���֮����С������˵�E�����ꣻ
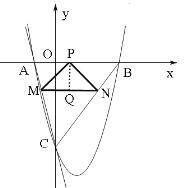
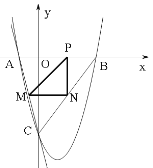
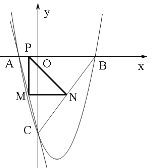
��3����ֱ��MNƽ����x�ᣬ�ֱ��߶�AC��BC�ڵ�M��N������x�����Ƿ���ڵ�P��ʹ�á�PMN�ǵ���ֱ�������Σ�������ڣ������������������P������ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��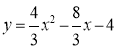 ����2��E
����2��E![]() ����3��
����3��![]() ��
��![]() ��
��![]()
��������
��1�����һ�κ���y =��4x��4�������ύ��A��C�����꣬���������߽���ʽ������⼴�ɣ�
��2����A����B���������߶Գ���x=1�Գƣ���B��E��C���㹲��ʱ����E����A�ľ����뵽��C�ľ���֮����С����y=0�����B�����꣬�ô���ϵ�������BC����ʽ��BC��Գ���Ľ��㼴ΪE�㣻
��3����ֱ�Ƕ�����з��࣬��3���������M��N��������Ϊa����ʾ����Ӧ�߶Σ��ٸ��ݵ���ֱ�������ε����ʽ�����⼴�ɣ�
�⣺��1����һ�κ���y=��4x��4��ͼ����x�ᡢy��ֱ���A��C���㣬
��A ����1��0����C ��0����4����
��A ����1��0����C ��0����4������![]() ��
��
��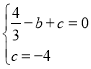 �����
����� ����
����
��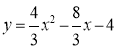 ��
��
��2����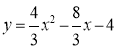 =
=![]() ��
��
�Գ�����ֱ��x=1��
��A, B����ֱ��x=1�Գ�
��ֱ��BC��Գ���ֱ��x=1�Ľ��㼴ΪE��
��ʱ��E����A�ľ����뵽��C�ľ���֮����С��
��y=0����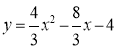 ����
����![]() ��
��
�����![]() ��
��![]() ��
��
��B![]() ����C
����C![]() ��
��
����ֱ��CB�Ľ���ʽΪ![]() ��
��
��x=1����![]() ����y=
����y=![]() ��
��
��E![]() ��
��
��3����DP��AB
��M��N��������Ϊa��
AC����ֱ�ߵĽ���ʽΪy=��4x��4, BC����ֱ�ߵĽ���ʽΪ��![]() ��
��
��M![]() ��N
��N![]() ��
��
�ٵ���PMN=90����MN=a+4��PM=��a����Ϊ�ǵ���ֱ�������Σ���a=a+4 ��a=��2 ��P�ĺ�����Ϊ![]() ��
��
��P������Ϊ![]() ��
��
�ڵ���PNM=90����PN=MN��ͬ�ϣ�a=��2����P�ĺ�����Ϊ![]() ��
��
��P������Ϊ![]() ��
��
�۵���MPN=90������MN���е�Q������PQ����PQ=��a��
��PM=PN����PQ��MN����MN=2PQ������a+4=��2a��
��ã�a=![]() ��
��
��P�ĺ�����Ϊ��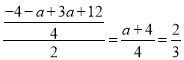 ����
����
��P�������Ϊ![]() ��
��
�ۺ�����P����Ϊ![]() ��
��![]() ��
��![]() ��
��


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
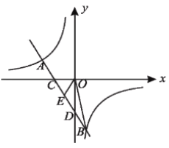
����Ŀ��˫����![]() ��kΪ��������
��kΪ��������![]() ����ֱ��
����ֱ��![]() ����
����![]() ����.
����.
��1����k��b��ֵ��
��2����ͼ��ֱ��AB��x���ڵ�C����y���ڵ�D������EΪCD���е㣬����BOE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����M��BA���ӳ����ϣ�

��1��������Ҫ����ͼ������ͼ�б�����Ӧ����ĸ���߹���ͼ��������ͼ�ۼ�����Ҫ��д������֤������
������MAC��ƽ����AN��
����AN�Ͻ�ȡAD=BC������CD��
��2���ڣ�1���������£��ж��ı���ABCD����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ�����ʦ������һ����Ŀ����ͼ��������һ�����������ֽƬABC�۳�һ���ԡ�AΪ�ڽǵ�������
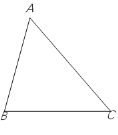
���õ��۷����£�
��һ�����۳���A��ƽ���ߣ���BC�ڵ�D��
�ڶ������۳�AD�Ĵ�ֱƽ���ߣ��ֱ�AB��AC�ڵ�E��F����ֽƬչƽ��
���������۳�DE��DF���õ��ı���AE
��������õ��۷���ͼ�л�����Ӧ��ͼ�Σ���֤���ı���AEDF�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���BPC�ǵȱ������Σ�BP��CP���ӳ��߷ֱ�AD�ڵ�E��F������BD��DP��BD��CF�ཻ�ڵ�H���������н��ۣ�
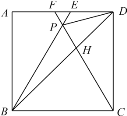
�١�ABE�ա�DCF������PDF=15������![]() ����
����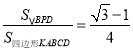 ,������ȷ�Ľ����У� �� ��
,������ȷ�Ľ����У� �� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Դ�ѧϰ��̬��һֱ�ǽ��������߹�ע������֮һ��Ϊ����Ϫ�ؽ���ֽ����Ҷ����ز���ѧУ�ľ��꼶ѧ���Դ�ѧϰ��̬�Ƚ�����һ�γ�������(��ѧϰ̬�ȷ�Ϊ�����㼶��A������ѧϰ�ܸ���Ȥ��B������ѧϰ�ϸ���Ȥ��C������ѧϰ������Ȥ)���������������Ƴ�ͼ�ٺ�ͼ�ڵ�ͳ��ͼ(������)�������ͼ���ṩ����Ϣ������������⣺
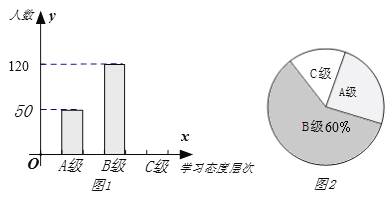
(1)�˴γ��������У���������______��ѧ����
(2)��ͼ�ٲ���������
(3)���ͼ����C����ռ��Բ�ĽǵĶ�����
(4)���ݳ�������Ľ��������������س���6000��ѧ�����ж�����ѧ��ѧϰ̬�ȴ��(������A����B��)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
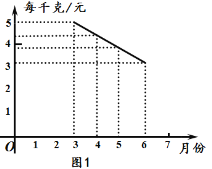
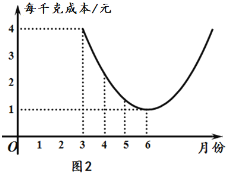
����Ŀ��ij���߲˵����۵���y1�������·�x֮��Ĺ�ϵ��ͼ1��ʾ���ɱ�y2�������·�x֮��Ĺ�ϵ��ͼ2��ʾ.
(1)��֪6�·������߲˵ijɱ���ͣ���ʱ����ÿ�ɿ˵������Ƕ���Ԫ?(����=�ۼۣ��ɱ�)
(2)�ֱ����y1��y2��x֮��ĺ�����ϵʽ��
(3)�ĸ��³��������߲ˣ�ÿǧ�˵��������?˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AB=AC=10,��D��BC���ϵ�һ���㣨����B��C�غϣ�,��ADE=��B=�Ϧ�,DE��AB�ڵ�E,��tan�Ϧ�=0.75,�����µĽ��ۣ�
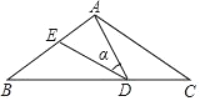
�١�DBE�ס�ACD���ڡ�ADE�ס�ACD���ۡ�BDEΪֱ��������ʱ,BDΪ8��3.5��
��0��BE��5.������ȷ�Ľ�����_______��������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��Բ�ڽ��ı���ABCD��AD��BC��AB�ǡ�O��ֱ����
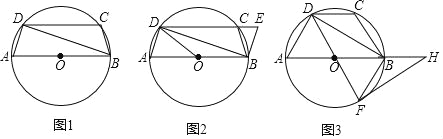
��1����֤��AB��CD��
��2����ͼ2������OD������CBE��2��ABD��BE��DC���ӳ����ڵ�E����AB��6��AD��2����CE�ij���
��3����ͼ3���ӳ�OBʹ��BH��OB��DF�ǡ�O��ֱ��������FH����BD��FH����֤��FH�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com