
【题目】双曲线![]() (k为常数,且
(k为常数,且![]() )与直线
)与直线![]() 交于
交于![]() 两点.
两点.
(1)求k与b的值;
(2)如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.
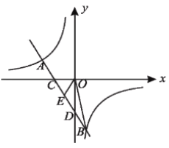
【答案】(1)![]() ;(2)S△BOE=
;(2)S△BOE= ![]() .
.
【解析】
(1)将A点的坐标代入一次函数解析式可得b的值,得到一次函数解析式再将B(1,n)代入一次函数解析式可得n的值,则求出点B(1,-4),将B(1,-4)代入反比例函数解析式可求出k的值.
(2)先求出点C、D两点的坐标,再求出E点坐标,所以S△BOE=S△ODE+S△ODB =![]() OD(xBxE),可求出△BOE的面积.
OD(xBxE),可求出△BOE的面积.
(1)∵点![]() 在直线
在直线![]() 上,
上,
∴![]()
∴![]() ,
,
∵点B(1,n)在直线![]() 上,
上,
∴![]()
∴B(1,-4),∵B(1,-4)在双曲线![]() 上,
上,
∴![]()
(2)∵直线AB的解析式为y=-2x-2,
令x=0,解得y=-2,令y=0,解得x=-1,
∴C(-1,0),D(0,-2),
∴S△COD=![]()
∵点E为CD的中点,
![]()
![]()
![]()
![]() .
.


科目:初中数学 来源: 题型:
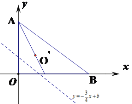
【题目】如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线![]() 对折,点O恰好落在∠OAB的平分线上的O’处,则
对折,点O恰好落在∠OAB的平分线上的O’处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
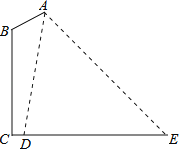
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从![]() 地出发,沿同一路线各自匀速向
地出发,沿同一路线各自匀速向![]() 地行驶,甲到达
地行驶,甲到达![]() 地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离
地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离![]() (千米)与乙车行驶时间
(千米)与乙车行驶时间![]() (小时)之间的函数图象如图所示,则下列结论错误的是( )
(小时)之间的函数图象如图所示,则下列结论错误的是( )
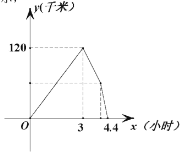
A.行驶3小时后,两车相距120千米
B.甲车从![]() 到
到![]() 的速度为100千米/小时
的速度为100千米/小时
C.甲车返回是行驶的速度为95千米/小时
D.![]() 、
、![]() 两地之间的距离为300千米
两地之间的距离为300千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市绿化工程进行招标,现有甲、乙两个工程队投标,已知甲队单独完成这项工程需要60天.经测算:如果甲队先做20天,再由甲队、乙队合作12天,那么此时共完成总工作量的![]() .
.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款4.5万元,乙队施工一天需付工程款2万元,该工程由甲乙两队合作若干天后,再由乙队完成剩余的工作,若要求完成此项工程的工程款不超过186万元,求甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 交于点
交于点![]() 点
点![]() 的坐标为
的坐标为![]() 轴于点
轴于点![]() .
.

(1)点![]() 的坐标为 ;
的坐标为 ;
(2)若点![]() 为
为![]() 的中点,求反比例函数
的中点,求反比例函数![]() 的解析式;
的解析式;
(3)在(2)条件下,以![]() 为边向右作正方形
为边向右作正方形![]() 交
交![]() 于点
于点![]() 直接写出
直接写出![]() 的周长与
的周长与![]() 的周长的比.
的周长的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=-x+1的图象与反比例函数![]() 的图象有一个交点是A(-1,n).
的图象有一个交点是A(-1,n).
(1)求反比例函数的解析式;
(2)M(d,![]() ),N(d,
),N(d,![]() )分别是一次函数和反比例函数图象上的两点,若
)分别是一次函数和反比例函数图象上的两点,若![]() ,求d的值.
,求d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )
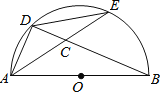
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y =﹣4x﹣4的图像与x轴、y轴分别交于A、C两点,抛物线y=![]() 的图像经过A、C两点,且与x轴交于点B.
的图像经过A、C两点,且与x轴交于点B.
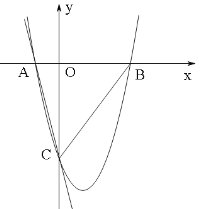
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上找一点E,使点E到点A的距离与到点C的距离之和最小,求出此点E的坐标;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com