
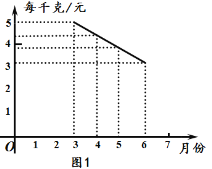
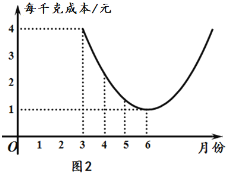
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每干克的收益是多少元?(收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
【答案】(1)6月份出售这种蔬菜每千克的收益是2元.(2)y1=﹣![]() +7;y2=
+7;y2=![]() x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
【解析】
(1)根据收益=售价-成本,由图像,得到当x=6时,y1=3,y2=1.所以,收益为2元.(2)根据图像设![]() ,
, ![]() .再代入点坐标进行作答.(3)由收益=售价-成本,得到收益= y1﹣y2,即﹣
.再代入点坐标进行作答.(3)由收益=售价-成本,得到收益= y1﹣y2,即﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13).化简,得到5月份出售这种蔬菜,每千克的收益最大.
x2﹣4x+13).化简,得到5月份出售这种蔬菜,每千克的收益最大.
解:(1)当x=6时,y1=3,y2=1,
∵y1﹣y2=3﹣1=2,
∴6月份出售这种蔬菜每千克的收益是2元.
(2)设![]() ,
, ![]() .
.
将(3,5)、(6,3)代入![]() ,
,
解得:
∴y1=﹣![]() +7;
+7;
将(3,4)代入y2=a(x﹣6)2+1,
4=a(3﹣6)2+1,解得:a=![]() ,
,
∴y2=![]() (x﹣6)2+1
(x﹣6)2+1
=![]() x2﹣4x+13.
x2﹣4x+13.
(3)5月份出售这种蔬菜,每千克的收益最大,理由:
∵y1﹣y2=﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)
=﹣![]() x2+
x2+![]()
![]() x﹣6
x﹣6
=﹣![]()
![]()
∴当x=5时,y1﹣y2取最大值,最大值为![]() ,
,
即5月份出售这种蔬菜,每千克的收益最大.


科目:初中数学 来源: 题型:
【题目】一次函数y=-x+1的图象与反比例函数![]() 的图象有一个交点是A(-1,n).
的图象有一个交点是A(-1,n).
(1)求反比例函数的解析式;
(2)M(d,![]() ),N(d,
),N(d,![]() )分别是一次函数和反比例函数图象上的两点,若
)分别是一次函数和反比例函数图象上的两点,若![]() ,求d的值.
,求d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
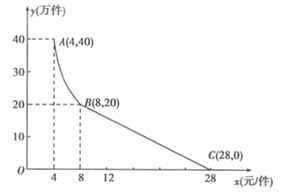
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y =﹣4x﹣4的图像与x轴、y轴分别交于A、C两点,抛物线y=![]() 的图像经过A、C两点,且与x轴交于点B.
的图像经过A、C两点,且与x轴交于点B.
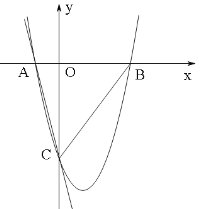
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上找一点E,使点E到点A的距离与到点C的距离之和最小,求出此点E的坐标;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点![]() ,用测角仪测出看塔顶
,用测角仪测出看塔顶![]() 的仰角
的仰角![]() ,在
,在![]() 点和塔之间选择一点
点和塔之间选择一点![]() ,测出看塔顶
,测出看塔顶![]() 的仰角
的仰角![]() ,然后用皮尺量出
,然后用皮尺量出![]() .
.![]() 两点的距离为
两点的距离为![]() m,自身的高度为
m,自身的高度为![]() m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(![]() ,结果保留整数).
,结果保留整数).
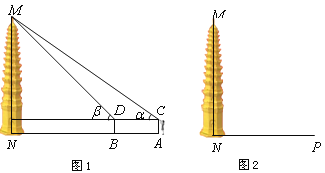
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影![]() 的长为
的长为![]() m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(![]() ,4),B(3,m)是直线AB与反比例函数
,4),B(3,m)是直线AB与反比例函数![]() (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
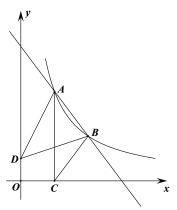
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直
垂直![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,与边
,与边![]() 相交于点
相交于点![]() ,
,![]() .
.
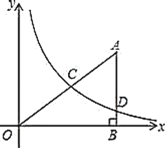
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)经过![]() 、
、![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
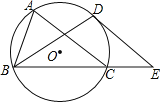
【题目】如图,△ABC为⊙O的内接三角形,∠ABC的角平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=![]() AC,求∠ACB的大小.
AC,求∠ACB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() ),与
),与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
(1)当![]() 时,
时,
①求抛物线的关系式;
②设点![]() 的横坐标为
的横坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的长,并求当
的长,并求当![]() 为何值时,
为何值时,![]() ?
?
(2)若![]() 长的最大值为16,试讨论关于
长的最大值为16,试讨论关于![]() 的一元二次方程
的一元二次方程![]() 的解的个数与
的解的个数与![]() 的取值范围的关系.
的取值范围的关系.
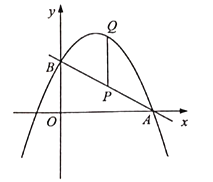
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com