
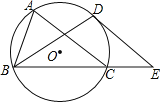
【题目】如图,△ABC为⊙O的内接三角形,∠ABC的角平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=![]() AC,求∠ACB的大小.
AC,求∠ACB的大小.
【答案】(1)见解析;(2)90°
【解析】
(1)连接OD交AC于H,因为∠ABC的角平分线交⊙O于点D,所以∠ABD=∠CBD,即![]() ,可得OD⊥AC,由DE∥AC,得OD⊥DE,进而得出DE为⊙O的切线;
,可得OD⊥AC,由DE∥AC,得OD⊥DE,进而得出DE为⊙O的切线;
(2)证明四边形CHDE为矩形,可得∠ACB=∠E=90°.
(1)如图,连接OD交AC于H,
∵∠ABC的角平分线交⊙O于点D,
∴∠ABD=∠CBD,
∴![]() ,
,
∴OD⊥AC,
∵DE∥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
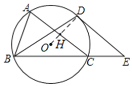
(2)∵OD⊥AC,
∴CH=![]() AC,
AC,
∵DE=![]() AC,
AC,
∴CH=DE,
∵DE∥AC,
∴四边形CHDE为平行四边形,
∵∠ODE=90°,
∴四边形CHDE为矩形,
∴∠ACB=∠E=90°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.

(1)按下列要求作图,并在图中标明相应的字母(尺规作图,保留作图痕迹,不要求写作法和证明);
①作∠MAC的平分线AN;
②在AN上截取AD=BC,连结CD.
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
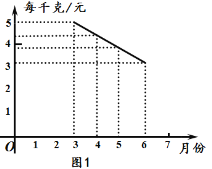
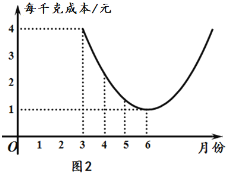
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每干克的收益是多少元?(收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论:
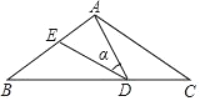
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或3.5;
④0<BE≤5.其中正确的结论是_______(填入正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
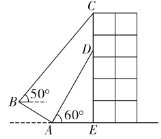
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
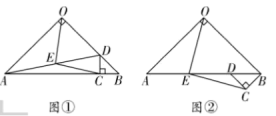
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
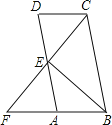
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
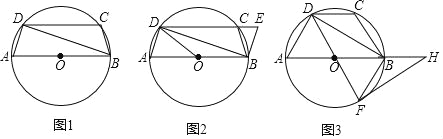
(1)求证:AB∥CD;
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com