
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论:
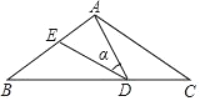
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或3.5;
④0<BE≤5.其中正确的结论是_______(填入正确结论的序号)
【答案】①③
【解析】①∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B∴∠ADC=180°﹣α﹣∠BDE,
∵∠BED=180°﹣α﹣∠BDE,∴∠BED=∠ADC∴△DBE∽△ACD,故①正确;
②∵∠B=∠C,∴∠C=∠ADE,不能得到△ADE∽△ACD;故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ABD,∴∠ADB=∠AED,
∵∠AED=90°,∴∠ADB=90°,即AD⊥BC,
∵AB=AC,∴BD=CD,∴∠ADE=∠B=α且cosα=0.8,AB=10,BD=8.
当∠BDE=90°时,易△BDE∽△CAD,∵∠BDE=90°,∴∠CAD=90°,
∵∠B=α且cosα=0.8.AB=10,∴cosC=0.8,∴CD=12.5,∴BD=BC﹣CD=3.5;故③正确.
④过A作AG⊥BC于G,∵cosα=0.8,∴BG=8,∴BC=16,易证得△BDE∽△CAD,
设BD=y,BE=x,∴ ![]() ,∴∴
,∴∴ ![]() ,整理得:y2﹣16y+64=64﹣10x,
,整理得:y2﹣16y+64=64﹣10x,
即(y﹣8)2=64﹣10x,∴0<x≤6.4.故④错误.故答案为:①③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(3a+2b)(3a-2b)-(3a-2b)2
(2)(a-5) 2-(a+6)(a-6)
(3)(3x-2y)2-(2x-y)(x-y)
(4)(-4a)·(2a2+3a-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
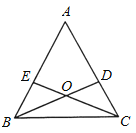
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
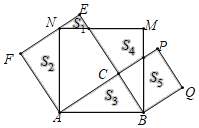
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班现要从A、B两位男生和C、D两位女生中,选派学生代表本班参加全校“中华好诗词”大赛.
(1)如果选派一位学生代表参赛,求选派到的代表是A的概率;
(2)如果选派两位学生代表参赛,求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com