
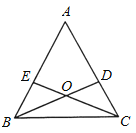
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
【答案】(1)详见解析;(2)直线AO垂直平分BC
【解析】
(1)根据对边对等角得到∠ABC=∠ACB,再结合角平分线的定义得到∠OBC=∠OCB,从而证明OB=OC;
(2)首先根据全等三角形的判定和性质得到OA平分∠BAC,再根据等腰三角形的三线合一的性质得到直线AO垂直平分BC.
(1)∵ 在△ABC中,AB=AC,
∴ ∠ABC=∠BCA,
∵ BD、CE分别平分∠ABC、∠BCA,
∴ ∠ABD=∠CBD ,∠ACE=∠BCE,
∴ ∠OBC=∠BCO,
∴ OB=OC,
∴ △OBC为等腰三角形;
(2)在△AOB与△AOC中,
∵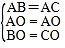 ,
,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,∴直线AO垂直平分BC.(等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合)


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过弧BD上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,TC=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
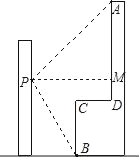
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两种手机上网计费方式,收费标准如下表所示:
计费方式 | 月使用费/元 | 包月上网时间/分 | 超时费/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
设上网时间为x分钟,
(1)若按方式A和方式B的收费金额相等,求x的值;
(2)若上网时间x超过320分钟,选择哪一种方式更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践
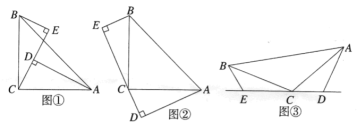
如图①,![]() ,垂足分别为点
,垂足分别为点![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)将![]() 所在直线旋转到
所在直线旋转到![]() 的外部,如图②,猜想
的外部,如图②,猜想![]() 之间的数量关系,直接写出结论,不需证明;
之间的数量关系,直接写出结论,不需证明;
(3)如图③,将图①中的条件改为:在![]() 中,
中,![]() 三点在同一直线上,并且
三点在同一直线上,并且![]() ,其中
,其中![]() 为任意钝角.猜想
为任意钝角.猜想![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年.某电动车商场为适应电动车进电梯的需求,需要购进100辆某型号的小型电动车供客户作宣传,经调查,该小型电动车2015年单价为2000元,2017年单价为1620元.
(1)求2015年到2017年该小型电动车单价平均每年降低的百分率;
(2)选购期间发现该小型电动车在A,B两个厂家有不同的促销方案,A厂家买十送一,B厂家全场打九折,试问去哪个厂家买更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
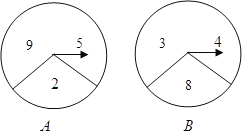
【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
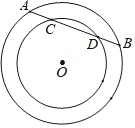
【题目】如图,在两个同心圆⊙O中,大圆的弦AB与小圆相交于C,D两点.
(1)求证:AC=BD;
(2)若AC=2,BC=4,大圆的半径R=5,求小圆的半径r的值;
(3)若ACBC等于12,请直接写出两圆之间圆环的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com