
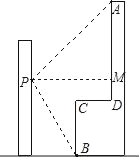
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
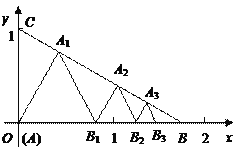
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第![]() 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
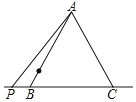
【题目】△ABC是边长为2的等边三角形,点P为直线BC上的动点,把线段AP绕A点逆时针旋转60°至AE,O为AB边上一动点,则OE的最小值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
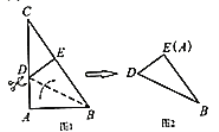
【题目】在三角形纸片![]() 中,
中,![]() ,
,![]() ,
,![]() .将该纸片沿过点
.将该纸片沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在斜边
落在斜边![]() 上的一点
上的一点![]() 处,折痕记为
处,折痕记为![]() (如图1),剪去
(如图1),剪去![]() 后得到双层
后得到双层![]() (如图2),再沿着边
(如图2),再沿着边![]() 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为__________cm.
某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
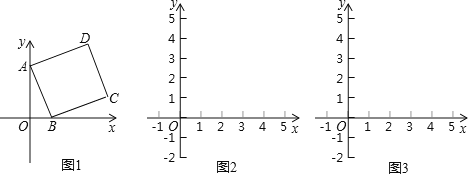
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
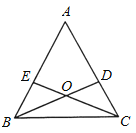
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
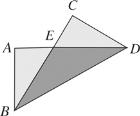
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com