
【题目】△ABC是边长为2的等边三角形,点P为直线BC上的动点,把线段AP绕A点逆时针旋转60°至AE,O为AB边上一动点,则OE的最小值为____.
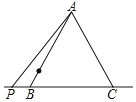
【答案】![]() .
.
【解析】
根据题意连接EC,作CH⊥AB于H,首先证明CE∥AB,再求出平行线之间的距离即可解决问题.
解:如图,连接EC,作CH⊥AB于H.
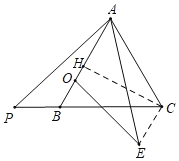
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=AC,
∵∠PAE=∠BAC=60°,
∴∠PAB=∠EAC,
∵PA=EQ,BA=CA,
∴△PAB≌△EAC(SAS),
∴∠ABP=∠ACE,
∵∠ABP=180°﹣60°=120°,
∴∠ACE=120°,
∴∠BCE=120°﹣60°=60°,
∴∠ABC=∠BCE,
∴CE∥AB,
∴点E的运动轨迹是直线CE(CE∥AB),
∵CB=CA=AB=2,CH⊥AB,
∴BH=AH=1,
∴CH![]() ,
,
根据垂线段最短,可知OE的最小值=CH![]() .
.
故答案为:![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
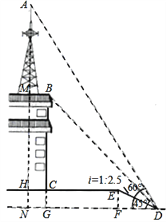
【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米。大家根据所学知识很快计算出了铁塔高AM。亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程。(数据![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过弧BD上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,TC=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
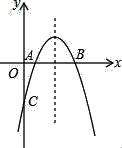
【题目】已知:如图所示,抛物线y=﹣x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)
(1)求抛物线的表达式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
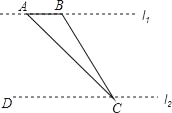
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
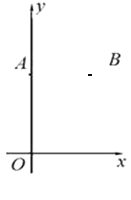
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:
①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
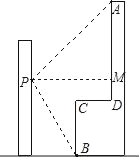
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年.某电动车商场为适应电动车进电梯的需求,需要购进100辆某型号的小型电动车供客户作宣传,经调查,该小型电动车2015年单价为2000元,2017年单价为1620元.
(1)求2015年到2017年该小型电动车单价平均每年降低的百分率;
(2)选购期间发现该小型电动车在A,B两个厂家有不同的促销方案,A厂家买十送一,B厂家全场打九折,试问去哪个厂家买更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com