
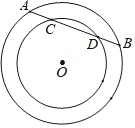
【题目】如图,在两个同心圆⊙O中,大圆的弦AB与小圆相交于C,D两点.
(1)求证:AC=BD;
(2)若AC=2,BC=4,大圆的半径R=5,求小圆的半径r的值;
(3)若ACBC等于12,请直接写出两圆之间圆环的面积.(结果保留π)
【答案】(1)见解析;(2)r为![]() ;(3)12π
;(3)12π
【解析】
(1)过O作OE⊥AB于点E,由垂径定理可知E为CD和AB的中点,则可证得结论;
(2)连接OC、OA,由条件可求得CD的长,则可求得CE和AE的长.在Rt△AOE中,利用勾股定理可求得OE的长.在Rt△COE中可求得OC的长;
(3)连接OA,OC,作OE⊥AB于点E,由垂径定理可得AE=BE.由勾股定理可得:OE2=OA2﹣AE2,OE2=OC2﹣CE2,继而可得OA2﹣OC2=AE2﹣CE2=(AE+CE)(AE﹣CE)=BCAC=12,则可求得圆环的面积.
(1)过O作OE⊥AB于点E,如图1,由垂径定理可得AE=BE,CE=DE,∴AE﹣CE=BE﹣DE,∴AC=BD;
(2)连接OC、OA,如图2.
∵AC=2,BC=4,∴AB=2+4=6,∴AE=3,∴CE=AE﹣AC=3﹣2=1.
在Rt△AOE中,由勾股定理可得OE2=OA2﹣AE2=52﹣32=16.
在Rt△COE中,由勾股定理可得:OC2=CE2+OE2=12+16=17,∴OC=![]() ,即小圆的半径r为
,即小圆的半径r为![]() ;
;
(3)连接OA,OC,作OE⊥AB于点E,如图2,由垂径定理可得AE=BE.
在Rt△AOE与Rt△OCE中:OE2=OA2﹣AE2,OE2=OC2﹣CE2,∴OA2﹣AE2=OC2﹣CE2,∴OA2﹣OC2=AE2﹣CE2=(AE+CE)(AE﹣CE)=(BE+CE)AC=BCAC=12,∴OA2﹣OC2=12,∴圆环的面积为:πOA2﹣πOC2=π(OA2﹣OC2)=12π.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
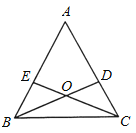
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
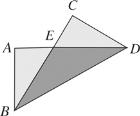
【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每个星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每个星期要少卖出10件;每降价1元,每个星期可多卖出20件.已知商品进价为每件40元,设每件商品的售价为x元(且x为正整数),每个星期的销售量为y件.
(1)求y与x的函数关系并直接写出自变量x的取值范围;
(2)设每星期的销售利润为W,请直接写出W与x的关系式;
(3)每件商品的售价定为多少元时,每个星期可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )

A. 4![]() cm2 B. 5
cm2 B. 5![]() cm2 C. 10
cm2 C. 10![]() cm2 D. 25
cm2 D. 25![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
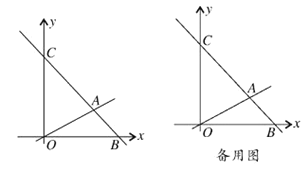
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,
,![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求点![]() 和点
和点![]() 的坐标.
的坐标.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com