
【题目】某商品现在的售价为每件60元,每个星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每个星期要少卖出10件;每降价1元,每个星期可多卖出20件.已知商品进价为每件40元,设每件商品的售价为x元(且x为正整数),每个星期的销售量为y件.
(1)求y与x的函数关系并直接写出自变量x的取值范围;
(2)设每星期的销售利润为W,请直接写出W与x的关系式;
(3)每件商品的售价定为多少元时,每个星期可获得最大利润?最大利润是多少元?
【答案】(1)![]() ;
;
(2)![]() ;(3)定价为65元时可获得最大利润为6250元
;(3)定价为65元时可获得最大利润为6250元
【解析】
(1)根据“每涨价1元,每个星期要少卖出10件;每降价1元,每个星期可多卖出20件”列出y与x的函数关系.
(2)设每星期所获利润为W,根据一星期利润等于每件的利润×销售量得到W与x的关系式;
(3)把(2)中解析式配成抛物线的顶点式,利用抛物线的最值问题即可得到答案.
(1)根据题意得:涨价时,y=300﹣10(x﹣60)(60≤x≤90),降价时,y=300+20(60﹣x)(40≤x<60),整理得:![]() ;
;
(2)当涨价时,y=(x﹣40)(﹣10x+900)(60≤x≤90),当降价时,y=(x﹣40)(﹣20x+1500)(40≤x<60);
综上所述:![]() ;
;
(3)当涨价时,W=(x﹣40)(﹣10x+900)=﹣10(x﹣65)2+6250(60≤x≤90),当x=65时,W的最大值是6250;
当降价时,W=(x﹣40)(﹣20x+1500)=﹣20(x﹣57.5)2+6125 (40≤x<60),所以定价为:x=57.5(元)时利润最大,最大值为6125元.
综合所述,定价为65元时可获得最大利润为6250元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).
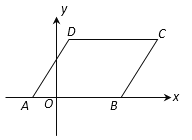
求:(1)点C的坐标;
(2)直线AC与y轴的交点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示:
(1)写出点A,B,C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以﹣1,请你在同一坐标系中描出对应的点A',B',C',并依次连接这三点,所得的△A'B'C'与原△ABC的位置关系是什么?
(3)在x轴上作出一点P,使得AP平分∠BAC.(保留作图痕迹,不写作法)
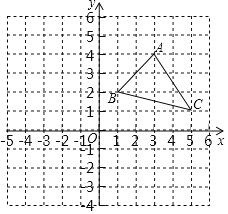
查看答案和解析>>
科目:初中数学 来源: 题型:
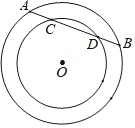
【题目】如图,在两个同心圆⊙O中,大圆的弦AB与小圆相交于C,D两点.
(1)求证:AC=BD;
(2)若AC=2,BC=4,大圆的半径R=5,求小圆的半径r的值;
(3)若ACBC等于12,请直接写出两圆之间圆环的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2anx+an2+n+3的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)对于任意非零实数a,存在确定的n的值,使抛物线与x轴有唯一的公共点,求此时n的值;
(3)当点P在x轴上时,抛物线与直线l的另一个交点Q,过点Q作x轴的平行线,交抛物线于点A,过点Q作y轴的平行线,交x轴于点B,求![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
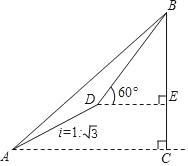
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com