
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧![]() 的中点,若△POC为直角三角形,则PB的长度( )
的中点,若△POC为直角三角形,则PB的长度( )
A. 1 B. 5 C. 1或5 D. 2或4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
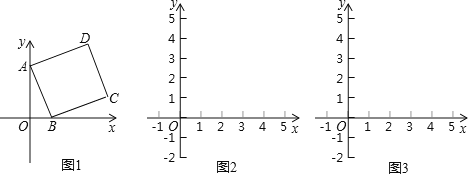
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
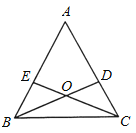
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店新进一种台灯.这种台灯的成本价为每个30元,经调查发现,这种台灯每天的销售量y(单位:个)是销售单价x(单位:元)(30≤x≤60)的一次函数.
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
(1)求销售量y与销售单价x之间的函数表达式;
(2)设这种台灯每天的销售利润为w元.这种台灯销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
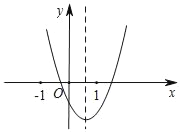
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每个星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每个星期要少卖出10件;每降价1元,每个星期可多卖出20件.已知商品进价为每件40元,设每件商品的售价为x元(且x为正整数),每个星期的销售量为y件.
(1)求y与x的函数关系并直接写出自变量x的取值范围;
(2)设每星期的销售利润为W,请直接写出W与x的关系式;
(3)每件商品的售价定为多少元时,每个星期可获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com