
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

【答案】(1)E(-3,4)、F(-5,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 连接OE,BF,根据题意可知:![]() 设
设![]() 则
则![]() 根据勾股定理可得:
根据勾股定理可得:![]() 即
即![]() 解得:
解得:![]() 即可求出点E的坐标,同理求出点F的坐标.
即可求出点E的坐标,同理求出点F的坐标.
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE,证明△BGE≌△OGF,证明四边形OEBF为菱形,令y=0,则![]() ,解得
,解得![]() , 根据菱形的性质得OF=OE=BE=BF=
, 根据菱形的性质得OF=OE=BE=BF=![]() 令y=n,则
令y=n,则![]() ,解得
,解得![]() 则CE=
则CE=![]() ,在Rt△COE中, 根据勾股定理列出方程
,在Rt△COE中, 根据勾股定理列出方程![]() ,即可求出点E的坐标,即可求出k的值;
,即可求出点E的坐标,即可求出k的值;
(3) 设EB=EO=x,则CE=-m-x,在Rt△COE中,根据勾股定理得到(-m-x)2+n2=x2,解得![]() ,求出点E(
,求出点E(![]() )、F(
)、F(![]() ),根据中点公式得到EF的中点为(
),根据中点公式得到EF的中点为(![]() ),将E(
),将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得![]() ,得m2=2n2
,得m2=2n2
即可求出tan∠EFO=![]() .
.
解:(1)如图:连接OE,BF,

E(-3,4)、F(-5,0)
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE

可证:△BGE≌△OGF(ASA)
∴BE=OF
∴四边形OEBF为菱形
令y=0,则![]() ,解得
,解得![]() ,∴OF=OE=BE=BF=
,∴OF=OE=BE=BF=![]()
令y=n,则![]() ,解得
,解得![]() ∴CE=
∴CE=![]()
在Rt△COE中,![]() ,
,
解得![]()
∴E(![]() )
)
∴![]()
(3) 设EB=EO=x,则CE=-m-x,
在Rt△COE中,(-m-x)2+n2=x2,解得![]()
∴E(![]() )、F(
)、F(![]() )
)
∴EF的中点为(![]() )
)
将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得
![]() ,得m2=2n2
,得m2=2n2
∴tan∠EFO=![]()


科目:初中数学 来源: 题型:
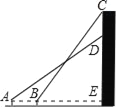
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
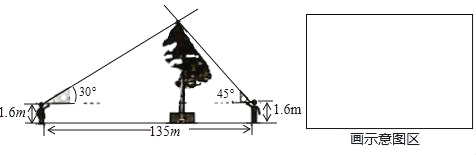
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
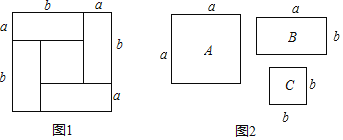
【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两种手机上网计费方式,收费标准如下表所示:
计费方式 | 月使用费/元 | 包月上网时间/分 | 超时费/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
设上网时间为x分钟,
(1)若按方式A和方式B的收费金额相等,求x的值;
(2)若上网时间x超过320分钟,选择哪一种方式更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB = 6cm,AD=10 cm,点P在AD 边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
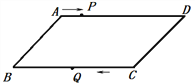
A. 1 次 B. 2次 C. 3次 D. 4次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
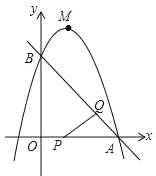
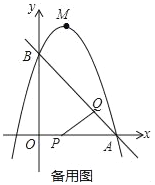
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
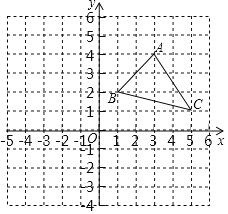
【题目】△ABC在平面直角坐标系中的位置如图所示:
(1)写出点A,B,C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以﹣1,请你在同一坐标系中描出对应的点A',B',C',并依次连接这三点,所得的△A'B'C'与原△ABC的位置关系是什么?
(3)在x轴上作出一点P,使得AP平分∠BAC.(保留作图痕迹,不写作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com