
【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
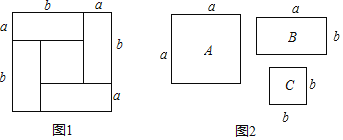
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .
【答案】(1)需要A卡片2张,B卡片3张,C卡片1张;(2)(a+2b);(a+3b).
【解析】
(1)按照多项式乘法的运算法则将(2a+b)(a+b)展开,则可得需要的A,B,C纸片的张数;
(2)先算出用1张A,5张B,6张C拼成一个长方形的面积,再将其因式分解,则可得这个长方形的边长.
(1)∵(2a+b)(a+b)=2a2+3ab+b2
而图片A,B,C的面积分别为:a2,ab,b2
∴需要A卡片2张,B卡片3张,C卡片1张.
(2)如果用1张A,5张B,6张C拼成一个长方形
则其面积为:a2+5ab+6b2;
∵a2+5ab+6b2=(a+2b)(a+3b)
∴这个长方形的边长分别是(a+2b)和(a+3b).
故答案为:(a+2b);(a+3b).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
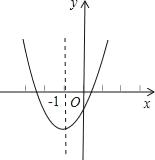
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac②abc>0③2a+b=0④a+b+c>0⑤a﹣b+c<0,则正确的结论的个数为( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, ∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,又分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
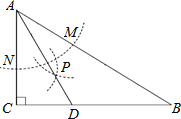
求证:(1)点D在AB的中垂线上.
(2)当CD=2时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
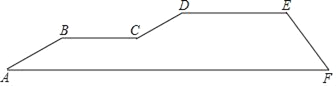
【题目】电影《厉害了,我的国》震撼上演后,引起了大家的强烈共鸣,当“复兴号”一幕又一幕的奔驰在祖国广袤的大地上,中国高铁的车轮快速的滚出了崭新中国的新画卷.中国高铁的飞速发展,使越来越多的人选择高铁出行.为了保证市民出行方便,某市的高铁站出入口与地铁站出入口进行对接.已知某人沿着坡角为30°的楼梯AB从A行至B,后沿BC路线上斜坡CD,坡角为30°,再行走一段距离DE,到达高铁入口处.若入口处楼梯EF的坡角为45°,DE∥BC∥AF,AB=20米,CD=4米,那么EF的长度是多少米?(保留0.1米)(![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
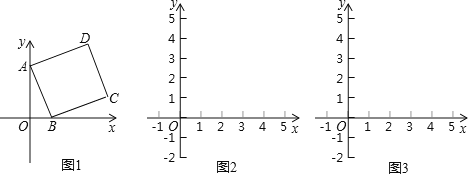
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动,P、Q两点从出发开始到__________秒时,点P和点Q的距离是10 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com