
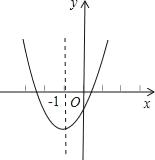
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac②abc>0③2a+b=0④a+b+c>0⑤a﹣b+c<0,则正确的结论的个数为( )
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
利用判别式的意义对①进行判断;抛物线开口方向得到a>0,利用抛物线的对称轴得到b=2a>0,利用抛物线与y轴的交点位置得到c<0,则可对②进行判断;利用抛物线的对称轴方程可对③进行判断;利用x=1,y>0可对④进行判断;利用x=﹣1,y<0可对⑤进行判断.
解:∵抛物线与x轴有2个交点,
∴b2﹣4ac>0,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线![]()
∴b=2a>0,即b﹣2a=0,所以③错误;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以②错误;
∵x=1时,y>0,
∴a+b+c>0,所以④正确;
∵x=﹣1时,y<0,
∴a﹣b+c<0,所以⑤正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
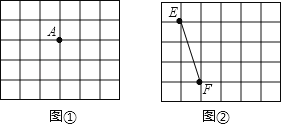
【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
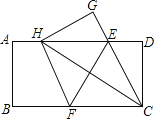
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 y-2 与 x+1 成正比例,当 x=7 时,y=6,
(1)写出 y 与 x 之间的函数关系式;
(2)当 y=-2 时,求 x 的值;
(3)若点 P(-6,m+4)在该函数图象上,求 m 的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,动点P从点A出发以每秒1个单位的速度沿AB向点B运动(点P不与点A,B重合),动点Q从点B出发以每秒2个单位的速度沿BC向点C运动,点P,Q同时出发,当点Q停止运动,点P也随之停止.连接AQ,交BD于点E,连接PE.设点P运动时间为x秒,求当x为何值时,△PBE≌△QBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
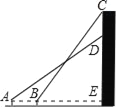
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
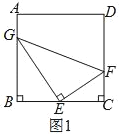
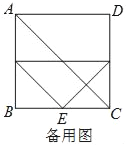
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
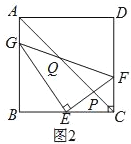
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
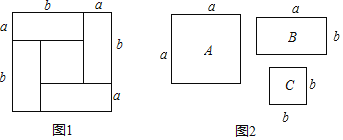
【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com