
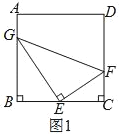
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
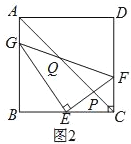
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.
【答案】(1)见解析;(2)y=4﹣x+![]() (0≤x≤3);(3)当△AGQ与△CEP相似,线段AG的长为2或4﹣
(0≤x≤3);(3)当△AGQ与△CEP相似,线段AG的长为2或4﹣![]() .
.
【解析】
(1)先判断出△BEF'≌△CEF,得出BF'=CF,EF'=EF,进而得出∠BGE=∠EGF,即可得出结论;
(2)先判断出△BEG∽△CFE进而得出CF=![]()
,即可得出结论;
(3)分两种情况,①△AGQ∽△CEP时,判断出∠BGE=60°,即可求出BG;
②△AGQ∽△CPE时,判断出EG∥AC,进而得出△BEG∽△BCA即可得出BG,即可得出结论.
(1)如图1,延长FE交AB的延长线于F',
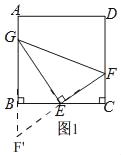
∵点E是BC的中点,
∴BE=CE=2,
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠F'=∠CFE,
在△BEF'和△CEF中,
 ,
,
∴△BEF'≌△CEF,
∴BF'=CF,EF'=EF,
∵∠GEF=90°,
∴GF'=GF,
∴∠BGE=∠EGF,
∵∠GBE=∠GEF=90°,
∴△GBE∽△GEF;
(2)∵∠FEG=90°,
∴∠BEG+∠CEF=90°,
∵∠BEG+∠BGE=90°,
∴∠BGE=∠CEF,
∵∠EBG=∠C=90°,
∴△BEG∽△CFE,
∴![]() ,
,
由(1)知,BE=CE=2,
∵AG=x,
∴BG=4﹣x,
∴![]() ,
,
∴CF=![]() ,
,
由(1)知,BF'=CF=![]() ,
,
由(1)知,GF'=GF=y,
∴y=GF'=BG+BF'=4﹣x+![]()
当CF=4时,即:![]() =4,
=4,
∴x=3,(0≤x≤3),
即:y关于x的函数表达式为y=4﹣x+![]() (0≤x≤3);
(0≤x≤3);
(3)∵AC是正方形ABCD的对角线,
∴∠BAC=∠BCA=45°,
∵△AGQ与△CEP相似,
∴①△AGQ∽△CEP,
∴∠AGQ=∠CEP,
由(2)知,∠CEP=∠BGE,
∴∠AGQ=∠BGE,
由(1)知,∠BGE=∠FGE,
∴∠AGQ=∠BGQ=∠FGE,
∴∠AGQ+∠BGQ+∠FGE=180°,
∴∠BGE=60°,
∴∠BEG=30°,
在Rt△BEG中,BE=2,
∴BG=![]() ,
,
∴AG=AB﹣BG=4﹣![]() ,
,
②△AGQ∽△CPE,
∴∠AQG=∠CEP,
∵∠CEP=∠BGE=∠FGE,
∴∠AQG=∠FGE,
∴EG∥AC,
∴△BEG∽△BCA,
∴![]() ,
,
∴![]() ,
,
∴BG=2,
∴AG=AB﹣BG=2,
即:当△AGQ与△CEP相似,线段AG的长为2或4﹣![]() .
.


科目:初中数学 来源: 题型:
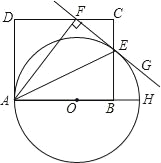
【题目】如图,AH是圆O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac②abc>0③2a+b=0④a+b+c>0⑤a﹣b+c<0,则正确的结论的个数为( )
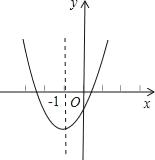
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,将这条直线进行平移后交
两点,将这条直线进行平移后交![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() ,要使点
,要使点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形面积为4,则直线
构成的四边形面积为4,则直线![]() 的解析式为__________.
的解析式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧![]() 的中点,若△POC为直角三角形,则PB的长度( )
的中点,若△POC为直角三角形,则PB的长度( )
A. 1 B. 5 C. 1或5 D. 2或4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
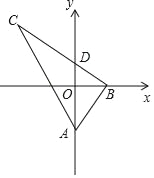
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, ∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,又分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
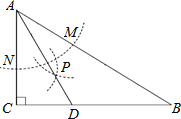
求证:(1)点D在AB的中垂线上.
(2)当CD=2时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
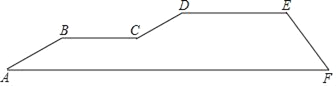
【题目】电影《厉害了,我的国》震撼上演后,引起了大家的强烈共鸣,当“复兴号”一幕又一幕的奔驰在祖国广袤的大地上,中国高铁的车轮快速的滚出了崭新中国的新画卷.中国高铁的飞速发展,使越来越多的人选择高铁出行.为了保证市民出行方便,某市的高铁站出入口与地铁站出入口进行对接.已知某人沿着坡角为30°的楼梯AB从A行至B,后沿BC路线上斜坡CD,坡角为30°,再行走一段距离DE,到达高铁入口处.若入口处楼梯EF的坡角为45°,DE∥BC∥AF,AB=20米,CD=4米,那么EF的长度是多少米?(保留0.1米)(![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com