
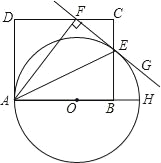
【题目】如图,AH是圆O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
【答案】(1)见解析;(2)⊙O的直径为![]() .
.
【解析】
(1)连接OE,证明FG是⊙O的切线,只要证明∠OEF=90°即可;
(2)先求出CE,利用角平分线得出EF=BE=5,进而求出CF,即可利用勾股定理求出AB,最后用勾股定理即可得出结论.
(1)如图1,连接OE,
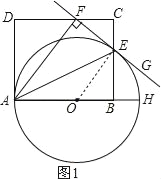
∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是⊙O的切线.
(2)设AB=x,
∵四边形ABCD是矩形,
∴AB=CD=x,BC=AD=8,
∴CE=BC﹣BE=3,
∵AE是∠BAF的角平分线,BE⊥AB,EF⊥AF,
∴EF=BE=5,
在Rt△CEF中,根据勾股定理得,CF=4,
∴DF=CD﹣CF=x﹣4,
在Rt△ABE和Rt△AFE中,![]() ,
,
∴Rt△ABE≌Rt△AFE(HL),
∴AF=AB=x,
在Rt△ADF中,x2﹣(x﹣4)2=64,
∴x=10,
∴AB=10,
设⊙O的半径为r,
∴OB=10﹣r,
在Rt△BOE中,r2﹣(10﹣r)2=25,
∴r=![]() ,
,
∴⊙O的直径为![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
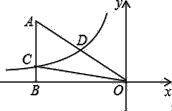
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
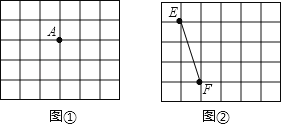
【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.
查看答案和解析>>
科目:初中数学 来源: 题型:
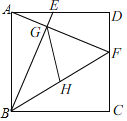
【题目】已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
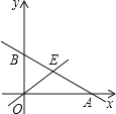
【题目】如图,直线y=-![]() x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
(1)求点E的坐标和b的值;
(2)在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=-![]() x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
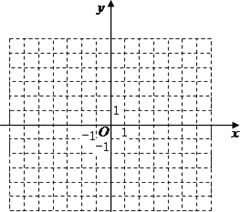
【题目】(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3,﹣5);D(﹣3,﹣5);E(3,5);
(2)A点到原点的距离是 .
(3)将点C向x轴的负方向平移6个单位,它与点 重合.
(4)连接CE,则直线CE与y轴是什么位置关系?
(5)点D分别到x、y轴的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
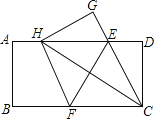
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
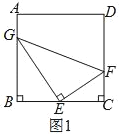
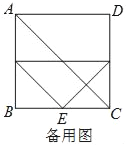
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
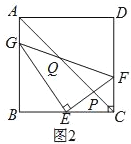
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com