
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
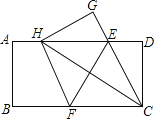
A. 1个 B. 2个 C. 3个 D. 4个
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
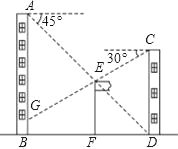
【题目】如图,在楼AB与楼CD之间有一旗杆EF,从AB顶部A点处经过旗杆顶部E点恰好看到楼CD的底部D点,且俯角为45°,从楼CD顶部C点处经过旗杆顶部E点恰好看到楼AB的G点,BG=1米,且俯角为30°,已知楼AB高20米,求旗杆EF的高度.(结果精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
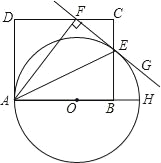
【题目】如图,AH是圆O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有3个红球、2个黄球和1个白球,每个球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)摸到的球的颜色可能是______;
(2)摸到概率最大的球的颜色是______;
(3)若将每个球都编上号码,分别记为1号球(红)、2号球(红)、3号球(红)、4号球(黄)、5号球(黄)、6号球(白),那么摸到1~6号球的可能性______(填相同或者不同);
(4)若在袋子中再放一些这样的黄球,从中任意摸出1个球,使摸到黄球的概率是![]() ,则放入的黄球个数是______.
,则放入的黄球个数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现规律:
特例1:![]() =
=![]() =
=![]() =
=![]() ;
;
特例2:![]() =
=![]() =
=![]() =
=![]() ;
;
特例3:![]() =4
=4![]() ;
;
特例4:______(填写一个符合上述运算特征的例子);
(2)归纳猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______;
(3)证明猜想:
(4)应用规律:
①化简:![]() ×
×![]() =______;
=______;
②若![]() =19
=19![]() ,(m,n均为正整数),则m+n的值为______.
,(m,n均为正整数),则m+n的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
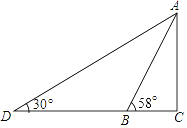
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac②abc>0③2a+b=0④a+b+c>0⑤a﹣b+c<0,则正确的结论的个数为( )
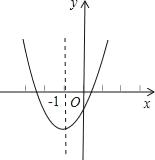
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,将这条直线进行平移后交
两点,将这条直线进行平移后交![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() ,要使点
,要使点![]() 、
、![]() 、
、![]() 、
、![]() 构成的四边形面积为4,则直线
构成的四边形面积为4,则直线![]() 的解析式为__________.
的解析式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
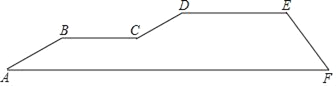
【题目】电影《厉害了,我的国》震撼上演后,引起了大家的强烈共鸣,当“复兴号”一幕又一幕的奔驰在祖国广袤的大地上,中国高铁的车轮快速的滚出了崭新中国的新画卷.中国高铁的飞速发展,使越来越多的人选择高铁出行.为了保证市民出行方便,某市的高铁站出入口与地铁站出入口进行对接.已知某人沿着坡角为30°的楼梯AB从A行至B,后沿BC路线上斜坡CD,坡角为30°,再行走一段距离DE,到达高铁入口处.若入口处楼梯EF的坡角为45°,DE∥BC∥AF,AB=20米,CD=4米,那么EF的长度是多少米?(保留0.1米)(![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com