
【题目】ABCD为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动,P、Q两点从出发开始到__________秒时,点P和点Q的距离是10 cm.

科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,动点P从点A出发以每秒1个单位的速度沿AB向点B运动(点P不与点A,B重合),动点Q从点B出发以每秒2个单位的速度沿BC向点C运动,点P,Q同时出发,当点Q停止运动,点P也随之停止.连接AQ,交BD于点E,连接PE.设点P运动时间为x秒,求当x为何值时,△PBE≌△QBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
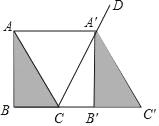
【题目】如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=![]() ,求CB的长.
,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
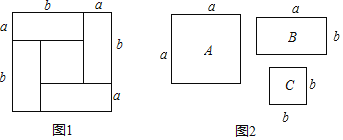
【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() .规定“把点
.规定“把点![]() 先作关于
先作关于![]() 轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点
轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点![]() 的坐标为_______;经过第二次变换后,点
的坐标为_______;经过第二次变换后,点![]() 的坐标为_____;那么连续经过2019次变换后,点
的坐标为_____;那么连续经过2019次变换后,点![]() 的坐标为_______.
的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB = 6cm,AD=10 cm,点P在AD 边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
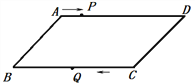
A. 1 次 B. 2次 C. 3次 D. 4次
查看答案和解析>>
科目:初中数学 来源: 题型:
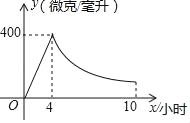
【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com