
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
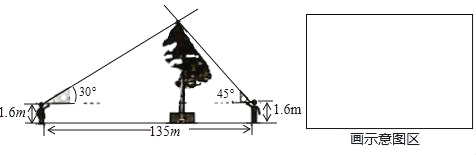
【答案】(1)详见解析;(2)小阳的说法正确.
【解析】
(1)如图,根据题意画出图形即可;
(2)由题意得,四边形CDEF是矩形,于是得到CD=BG=EF=1.6米,CF=DE=135米,设AG=x米,解直角三角形即可得到结论.
(1)如图,AB表示古松树的高,CD,EF分别表示小红和小阳的眼睛到地面的距离;
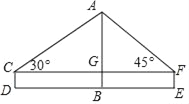
(2)由题意得,四边形CDEF是矩形,
∴CD=BG=EF=1.6米,CF=DE=135米,
设AG=x米,
∵∠ACG=30°,∠AFG=45°,∠AGC=∠AGF=90°,
∴GF=AG=x,AC=2AG=2x,
∴![]() 米,
米,
∴DE=BD+BE=CG+GF=![]()
∴x≈49.45,
∴AB=AG+GB=51.1米,
∴古松树高=51.1米<60米,
∴小阳的说法正确.


科目:初中数学 来源: 题型:
【题目】(1)发现规律:
特例1:![]() =
=![]() =
=![]() =
=![]() ;
;
特例2:![]() =
=![]() =
=![]() =
=![]() ;
;
特例3:![]() =4
=4![]() ;
;
特例4:______(填写一个符合上述运算特征的例子);
(2)归纳猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______;
(3)证明猜想:
(4)应用规律:
①化简:![]() ×
×![]() =______;
=______;
②若![]() =19
=19![]() ,(m,n均为正整数),则m+n的值为______.
,(m,n均为正整数),则m+n的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧![]() 的中点,若△POC为直角三角形,则PB的长度( )
的中点,若△POC为直角三角形,则PB的长度( )
A. 1 B. 5 C. 1或5 D. 2或4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, ∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,又分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
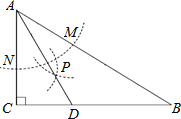
求证:(1)点D在AB的中垂线上.
(2)当CD=2时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影《厉害了,我的国》震撼上演后,引起了大家的强烈共鸣,当“复兴号”一幕又一幕的奔驰在祖国广袤的大地上,中国高铁的车轮快速的滚出了崭新中国的新画卷.中国高铁的飞速发展,使越来越多的人选择高铁出行.为了保证市民出行方便,某市的高铁站出入口与地铁站出入口进行对接.已知某人沿着坡角为30°的楼梯AB从A行至B,后沿BC路线上斜坡CD,坡角为30°,再行走一段距离DE,到达高铁入口处.若入口处楼梯EF的坡角为45°,DE∥BC∥AF,AB=20米,CD=4米,那么EF的长度是多少米?(保留0.1米)(![]() ≈1.414)
≈1.414)
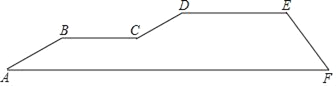
查看答案和解析>>
科目:初中数学 来源: 题型:
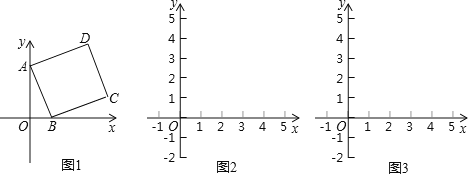
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
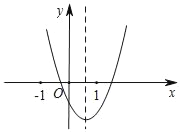
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com