
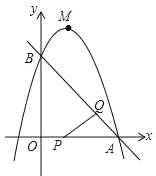
����Ŀ����ͼ����ֱ֪��y=��x+3��x�ᡢy��ֱ���A��B���㣬������y=��x2+bx+c����A��B���㣬��P���߶�OA�ϣ��ӵ�A��1����λ/����ٶ������˶���ͬʱ����Q���߶�AB�ϣ��ӵ�A���������B��![]() ����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ����APQΪֱ�������Σ�
��3������P��PE��y�ᣬ��AB�ڵ�E������Q��QF��y�ᣬ���������ڵ�F������EF����EF��PQʱ�����F�����꣮
���𰸡���1�������ߵĽ���ʽΪy=��x2+2x+3����2����t=1��t=![]() ʱ����PQA��ֱ�������Σ���3����F������Ϊ��2��3����
ʱ����PQA��ֱ�������Σ���3����F������Ϊ��2��3����
�������������������1��������ֱ�߽���ʽȷ��A���B�����꣬Ȼ�����ô���ϵ�����������ߵĽ���ʽ��
��2��OP=t��AQ=![]() t����PA=3-t�����жϡ�QAP=45�������ۣ�����PQA=90��ʱ����ͼ�٣����õ���ֱ�������ε����ʵ�PA=
t����PA=3-t�����жϡ�QAP=45�������ۣ�����PQA=90��ʱ����ͼ�٣����õ���ֱ�������ε����ʵ�PA=![]() AQ����3-t=
AQ����3-t=![]()
![]() t������APQ=90��ʱ����ͼ�������õ���ֱ�������ε����ʵ�AQ=
t������APQ=90��ʱ����ͼ�������õ���ֱ�������ε����ʵ�AQ=![]() AP����
AP����![]() t=
t=![]() ��3-t����Ȼ��ֱ�����t�ķ��̼��ɣ�
��3-t����Ȼ��ֱ�����t�ķ��̼��ɣ�
��3����ͼ�ۣ��ӳ�FQ��x���ڵ�H�����P������Ϊ��t��0�������E������Ϊ��t��-t+3��������AQHΪ����ֱ�������Σ���AH=HQ=![]() AQ=t����ɱ�ʾ����Q������Ϊ��3-t��t������F������Ϊ[3-t��-��3-t��2+2��3-t��+3��]������FQ=-t2+3t����֤���ı���PQFEΪƽ���ı��εõ�EP=FQ����3-t=3t-t2��Ȼ��ⷽ�����t���ɵõ���F������.
AQ=t����ɱ�ʾ����Q������Ϊ��3-t��t������F������Ϊ[3-t��-��3-t��2+2��3-t��+3��]������FQ=-t2+3t����֤���ı���PQFEΪƽ���ı��εõ�EP=FQ����3-t=3t-t2��Ȼ��ⷽ�����t���ɵõ���F������.
�����������1����y=��x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
�൱y=0ʱ��x=3����A������Ϊ��3��0������x=0ʱ��y=3����B������Ϊ��0��3����
�߽�A��3��0����B��0��3������ã� ![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��2����OA=OB=3����BOA=90����
���QAP=45����
��ͼ����ʾ����PQA=90��ʱ��

���˶�ʱ��Ϊt�룬��QA=![]() t��PA=3��t��
t��PA=3��t��
��Rt��PQA�� ![]() ����
����![]() ��
��
��ã�t=1��
��ͼ����ʾ����QPA=90��ʱ��
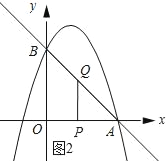
���˶�ʱ��Ϊt�룬��QA=![]() t��PA=3��t��
t��PA=3��t��
��Rt��PQA�� ![]() ����
����![]() ��
��
��ã�t=![]() ��
��
������������t=1��t=![]() ʱ����PQA��ֱ�������Σ�
ʱ����PQA��ֱ�������Σ�
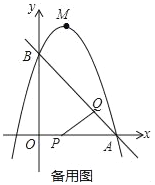
��3����ͼ����ʾ��

���P��������t��0�������E��������t����t+3������EP=3��t����Q��������3��t��t������F��������3��t������3��t��2+2��3��t��+3������F��3��t��4t��t2������FQ=4t��t2��t=3t��t2��
��EP��FQ��EF��PQ��
���ı���EFQPΪƽ���ı��Σ�
��EP=FQ����3��t=3t��t2��
��ã�t1=1��t2=3����ȥ����
��t=1����õ�F������Ϊ��2��3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90���� ��B=30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ֱַ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��
MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��
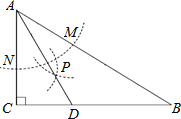
��֤����1����D��AB���д����ϣ�
��2����CD=2ʱ������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�ı�OA��OC�ֱ���x�ᡢy���ϣ���B������Ϊ(m��n)��m��0��
n��0����E���ڱ�BC�ϣ�F���ڱ�OA�ϣ�������OABC��EF�۵�����B�������O�غϣ�˫����![]() ����E.
����E.
(1) ��m����8��n ��4��ֱ��д��E��F�����ꣻ
(2) ��ֱ��EF�Ľ���ʽΪ![]() ����k��ֵ��
����k��ֵ��
(3) ��˫����![]() ��EF���е㣬ֱ��д��tan��EFO��ֵ.
��EF���е㣬ֱ��д��tan��EFO��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����С���ƻ���һ�鳤Ϊ20�ף���12�ľ��γ��������������ഹֱ�ij������·��һ���M�����������Һ�������Ŀ��ȱ�Ϊ3��2�������ಿ���ֻ��ݣ���Ҫʹ�ֻ��ݵ�����ﵽ144��2���������·��Ϊ_____�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��½�һ��̨�ƣ�����̨�Ƶijɱ���Ϊÿ��30Ԫ�������鷢�֣�����̨��ÿ���������y����λ�����������۵���x����λ��Ԫ����30��x��60����һ�κ�����
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
��1����������y�����۵���x֮��ĺ�������ʽ��
��2��������̨��ÿ�����������ΪwԪ������̨�����۵��۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���ı���ABCDΪƽ���ı��Σ�AD=a��ACΪ�Խ��ߣ�BM��AC������D�� DE��CM����AC���ӳ�����F����BM���ӳ�����E��
��1����֤����ADF�ա�BCM��
��2����AC=2CF����ADC=60����AC��DC�����ı���ABED��������ú�a�Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���abc��0����2a+b��0����b2��4ac��0����a��b+c��0��������ȷ�ĸ����ǣ�������
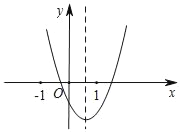
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ɾ���(��������)���ڽ�ƽ������Χ�ɵ��ı���һ����(����)
A. ƽ���ı��� B. ���� C. ���� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
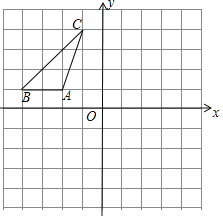
����Ŀ����ƽ��ֱ������ϵ�У���ͼ��ʾA����2��1����B����4��1����C����1��4����
��1����ABC����ƽ��һ����λ��������ƽ��һ����λ�õ���A1B1C1����ôC�Ķ�Ӧ��C1������Ϊ_____��P�㵽��ABC��������ľ�����ȣ���P������Ϊ______��
��2����ABC���ڵ�һ����ƽ�������ڵ�ֱ������ԳƱ任�õ���A2B2C2����ô��B�Ķ�Ӧ��B2������Ϊ______��
��3����A3B3C3�ǡ�ABC������ƽ���ڵ�Q��˳ʱ����ת�õ��ģ���A3��1��0����B3��1��2����C3��4����1������Q������Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com