
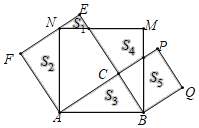
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
【答案】5
【解析】
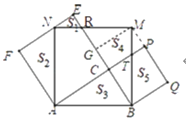
如图,连接MQ,作MG⊥EC于G,设PC交BM于T,MN交EC于R.证明△ABC≌△MBQ(SAS),推出∠ACB=∠BQM=90°,由∠PQB=90°,推出M,P,Q共线,由四边形CGMP是矩形,推出MG=PC=BC,证明△MGR≌△BCT(AAS),推出MR=BT,由MN=BM,NR=MT,可证△NRE≌MTP,推出S1+S5=S3=5.
解:如图,连接MQ,作MG⊥EC于G,设PC交BM于T,MN交EC于R.
∵∠ABM=∠CBQ=90°,
∴∠ABC=∠MBQ,
∵BA=BM,BC=BQ,
∴△ABC≌△MBQ(SAS),
∴∠ACB=∠MQB=90°,
∵∠PQB=90°,
∴M,P,Q共线,
∵四边形CGMP是矩形,
∴MG=PC=BC,
∵∠BCT=∠MGR=90°,∠BTC+∠CBT=90°,∠BQM+∠CBT=90°,
∴∠MRG=∠BTC,
∴△MGR≌△BCT(AAS),
∴MR=BT,
∵MN=BM,
∴NR=MT,
∵∠MRG=∠BTC,
∴∠NRE=∠MTP,
∵∠E=∠MPT=90°,则△NRE≌MTP(AAS),
∴S1+S5=S3=5.
故答案为:5.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
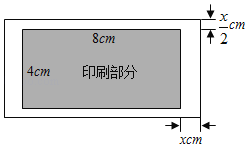
【题目】如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各![]() cm,左右空白宽各xcm,四周空白处的面积为Scm2.
cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论:
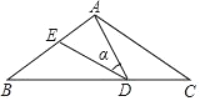
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或3.5;
④0<BE≤5.其中正确的结论是_______(填入正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
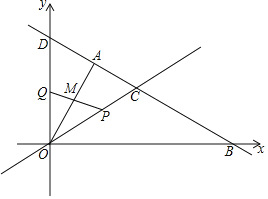
【题目】如图,在平面直角坐标系中,直线AB经过点A(![]() ,
,![]() )和B (2
)和B (2![]() ,0),且与y轴交于点D,直线OC与AB交于点C,且点C的横坐标为
,0),且与y轴交于点D,直线OC与AB交于点C,且点C的横坐标为![]() .
.
(1)求直线AB的解析式;
(2)连接OA,试判断△AOD的形状;
(3)动点P从点C出发沿线段CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点O出发沿y轴的正半轴以相同的速度运动,当点Q到达点D时,P,Q同时停止运动.设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场花9万元从厂家购买A型和B型两种型号的电视机共50台,其中A型电视机的进价为每台1500元,B型电视机的进价为每台2500元.
(1)求该商场购买A型和B型电视机各多少台?
(2)若商场A型电视机的售价为每台1700元,B型电视机的售价为每台2800元,不考虑其他因素,那么销售完这50台电视机该商场可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
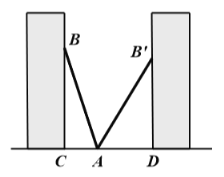
【题目】如图,小巷左右两侧是竖直的墙,一架梯子![]() 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离![]() 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离![]() 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离![]() 为2米,求小巷的宽度
为2米,求小巷的宽度![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com