
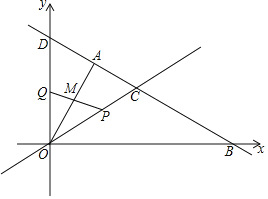
【题目】如图,在平面直角坐标系中,直线AB经过点A(![]() ,
,![]() )和B (2
)和B (2![]() ,0),且与y轴交于点D,直线OC与AB交于点C,且点C的横坐标为
,0),且与y轴交于点D,直线OC与AB交于点C,且点C的横坐标为![]() .
.
(1)求直线AB的解析式;
(2)连接OA,试判断△AOD的形状;
(3)动点P从点C出发沿线段CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点O出发沿y轴的正半轴以相同的速度运动,当点Q到达点D时,P,Q同时停止运动.设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.
【答案】(1)y=﹣![]() x+2;(2)△AOD为直角三角形,理由见解析;(3)t=
x+2;(2)△AOD为直角三角形,理由见解析;(3)t=![]() 或
或![]() .
.
【解析】
(1)将点A、B的坐标代入一次函数表达式:y=kx+b,即可求解;
(2)由点A、O、D的坐标得:AD2=1,AO2=3,DO2=4,故DO2=OA2+AD2,即可求解;
(3)点C(![]() ,1),∠DBO=30°,则∠ODA=60°,则∠DOA=30°,故点C(
,1),∠DBO=30°,则∠ODA=60°,则∠DOA=30°,故点C(![]() ,1),则∠AOC=30°,∠DOC=60°,OQ=CP=t,则OP=2﹣t.①当OP=OM时,OQ=QH+OH,即
,1),则∠AOC=30°,∠DOC=60°,OQ=CP=t,则OP=2﹣t.①当OP=OM时,OQ=QH+OH,即![]() (2﹣t)+
(2﹣t)+![]() (2﹣t)=t,即可求解;②当MO=MP时,∠OQP=90°,故OQ=
(2﹣t)=t,即可求解;②当MO=MP时,∠OQP=90°,故OQ=![]() OP,即可求解;③当PO=PM时,故这种情况不存在.
OP,即可求解;③当PO=PM时,故这种情况不存在.
解:(1)将点A、B的坐标代入一次函数表达式:y=kx+b得: 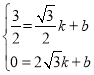 ,
,
解得: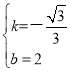 ,
,
故直线AB的表达式为:y=﹣![]() x+2;
x+2;
(2)直线AB的表达式为:y=﹣![]() x+2,则点D(0,2),
x+2,则点D(0,2),
由点A、O、D的坐标得:AD2=1,AO2=3,DO2=4,
故DO2=OA2+AD2,
故△AOD为直角三角形;
(3)直线AB的表达式为:y=﹣![]() x+2,故点C(
x+2,故点C(![]() ,1),则OC=2,
,1),则OC=2,
则直线AB的倾斜角为30°,即∠DBO=30°,则∠ODA=60°,则∠DOA=30°
故点C(![]() ,1),则OC=2,
,1),则OC=2,
则点C是AB的中点,故∠COB=∠DBO=30°,则∠AOC=30°,∠DOC=60°,
OQ=CP=t,则OP=OC﹣PC=2﹣t,
①当OP=OM时,如图1,
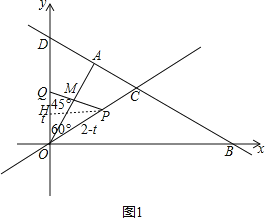
则∠OMP=∠MPO=![]() (180°﹣∠AOC)=75°,故∠OQP=45°,
(180°﹣∠AOC)=75°,故∠OQP=45°,
过点P作PH⊥y轴于点H,
则OH=![]() OP=
OP=![]() (2﹣t),
(2﹣t),
由勾股定理得:PH=![]() (2﹣t)=QH,
(2﹣t)=QH,
OQ=QH+OH=![]() (2﹣t)+
(2﹣t)+![]() (2﹣t)=t,
(2﹣t)=t,
解得:t=![]() ;
;
②当MO=MP时,如图2,
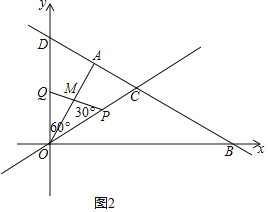
则∠MPO=∠MOP=30°,而∠QOP=60°,
∴∠OQP=90°,
故OQ=![]() OP,即t=
OP,即t=![]() (2﹣t),
(2﹣t),
解得:t=![]() ;
;
③当PO=PM时,
则∠OMP=∠MOP=30°,而∠MOQ=30°,
故这种情况不存在;
综上,t=![]() 或
或![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】哈市某专卖店销售某品牌服装,该服装进价为每件80元,当每件服装售价为240元时,月销售量为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现,当销售单价每降价10元,月销量就增加20件.设每件服装售价为x元,该专卖店的月销售量为y件.
(1)求y与x的关系式;
(2)在某月进货时,该专卖店进货款不超过18000元,售价定为多少元可使月利润达到33000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
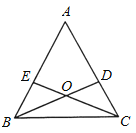
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
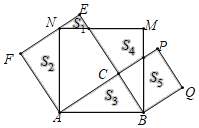
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班现要从A、B两位男生和C、D两位女生中,选派学生代表本班参加全校“中华好诗词”大赛.
(1)如果选派一位学生代表参赛,求选派到的代表是A的概率;
(2)如果选派两位学生代表参赛,求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com