
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
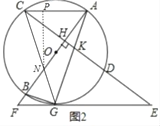
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

【答案】(1)证明见解析;(2)证明见解析;(3)CN=![]() .
.
【解析】试题分析:
(1)连接OG,则由已知易得∠OGE=∠AHK=90°,由OG=OA可得∠AGO=∠OAG,从而可得∠KGE=∠AKH=∠EKG,这样即可得到KE=GE;
(2)设∠FGB=α,由AB是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE可得∠EKG=90°-α,这样在△GKE中可得∠E=2α,由∠FGB=![]() ∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;
(3)如下图2,作NP⊥AC于P,
由(2)可知∠ACH=∠E,由此可得sinE=sin∠ACH=![]() ,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=
,设AH=3a,可得AC=5a,CH=4a,则tan∠CAH=![]() ,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=
,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC,从而可得CK=AC=5a,由此可得HK=a,tan∠AKH=![]() ,AK=
,AK=![]() a,结合AK=
a,结合AK=![]() 可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
可得a=1,则AC=5;在四边形BGKH中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG可得∠ACG=∠AKH,
在Rt△APN中,由tan∠CAH=![]() ,可设PN=12b,AP=9b,由tan∠ACG=
,可设PN=12b,AP=9b,由tan∠ACG=![]() tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=
tan∠AKH=3可得CP=4b,由此可得AC=AP+CP=![]() =5,则可得b=
=5,则可得b=![]() ,由此即可在Rt△CPN中由勾股定理解出CN的长.
,由此即可在Rt△CPN中由勾股定理解出CN的长.
试题解析:
(1)如图1,连接OG.
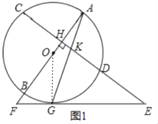
∵EF切⊙O于G,
∴OG⊥EF,
∴∠AGO+∠AGE=90°,
∵CD⊥AB于H,
∴∠AHD=90°,
∴∠OAG=∠AKH=90°,
∵OA=OG,
∴∠AGO=∠OAG,
∴∠AGE=∠AKH,
∵∠EKG=∠AKH,
∴∠EKG=∠AGE,
∴KE=GE.
(2)设∠FGB=α,
∵AB是直径,
∴∠AGB=90°,
∴∠AGE=∠EKG=90°﹣α,
∴∠E=180°﹣∠AGE﹣∠EKG=2α,
∵∠FGB=![]() ∠ACH,
∠ACH,
∴∠ACH=2α,
∴∠ACH=∠E,
∴CA∥FE.
(3)作NP⊥AC于P.
∵∠ACH=∠E,
∴sin∠E=sin∠ACH=![]() ,设AH=3a,AC=5a,
,设AH=3a,AC=5a,
则CH=![]() ,tan∠CAH=
,tan∠CAH=![]() ,
,
∵CA∥FE,
∴∠CAK=∠AGE,
∵∠AGE=∠AKH,
∴∠CAK=∠AKH,
∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=![]() =3,AK=
=3,AK= ![]() ,
,
∵AK=![]() ,
,
∴![]() ,
,
∴a=1.AC=5,
∵∠BHD=∠AGB=90°,
∴∠BHD+∠AGB=180°,
在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,
∴∠ABG+∠HKG=180°,
∵∠AKH+∠HKG=180°,
∴∠AKH=∠ABG,
∵∠ACN=∠ABG,
∴∠AKH=∠ACN,
∴tan∠AKH=tan∠ACN=3,
∵NP⊥AC于P,
∴∠APN=∠CPN=90°,
在Rt△APN中,tan∠CAH=![]() ,设PN=12b,则AP=9b,
,设PN=12b,则AP=9b,
在Rt△CPN中,tan∠ACN=![]() =3,
=3,
∴CP=4b,
∴AC=AP+CP=13b,
∵AC=5,
∴13b=5,
∴b=![]() ,
,
∴CN=![]() =
= ![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】李先生从家到公司去上班要先经过一段平路再过一段下坡路。他走平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,从家到公司需要10分钟,从公司到家里需要14分钟,求李先生家离公司多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某集团公司对所属甲、乙两分厂下半年经营情况记录(其中“+”表示盈利,“-”表示亏损,单位:亿元)如下表.
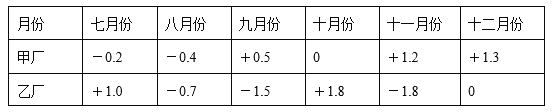
(1)计算八月份乙厂比甲厂多亏损多少亿元?
(2)分别计算下半年甲、乙两个工厂平均每月盈利或亏损多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:

(1)菜地的长a=___米,宽b=___米;
(2)菜地的面积S=___平方米;
(3)求当x=1米时,菜地的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
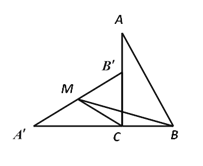
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 2.将△ABC绕顶点C逆时针旋转得到△![]() 使点
使点![]() 落在AC边上.设M是
落在AC边上.设M是![]() 的中点,连接BM,CM,则△BCM的面积为( )
的中点,连接BM,CM,则△BCM的面积为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com