
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:

(1)菜地的长a=___米,宽b=___米;
(2)菜地的面积S=___平方米;
(3)求当x=1米时,菜地的面积。
【答案】(1)18-2x,10-x;(2)(18-2x)(10-x);(3)144m2.
【解析】
(1)本题可先根据所给的图形,即可得出菜地的长和宽,
(2)由(1)根据长方形面积公式即可求出面积;
(3)第三问可以直接将x=1代入第二问所求的面积式子中,得出结果.
(1)∵其余三面留出宽都是x米的小路,
∴由图可以看出:菜地的长为18-2x米,宽为10-x米;
(2)由(1)知:菜地的长为18-2x米,宽为10-x米,
所以菜地的面积为S=(18-2x)(10-x);
(3)由(2)得菜地的面积为:S=(18-2x)(10-x),
当x=1时,S=(18-2)(10-1)=144m2.
故答案分别为:(1)18-2x,10-x;(2)(18-2x)(10-x);(3)144m2.


科目:初中数学 来源: 题型:
【题目】我县盛产不知火和脐橙两种水果 ,某公司计划用两种型号的汽车运输不知火和脐橙到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装运不知火,2辆汽车装运脐橙可共装载33吨,若用2辆汽车装运不知火,3辆汽车装运脐橙可共装载32吨.
(1)求每辆汽车可装载不知火或脐橙各多少吨?
(2)据调查,全部销售完后,每吨不知火可获利700元,每吨脐橙可获利500元,计划用20辆汽车运输,且脐橙不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l 1,l 2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )

A.乙摩托车的速度较快B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地![]() kmD.经过
kmD.经过![]() 小时两摩托车相遇
小时两摩托车相遇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位,得到△A1B1C1,把这两步操作规定为翻移变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(1,1),(3,1).把△ABC经过连续3次翻移变换得到△A3B3C3,则点A的对应点A3的坐标是( )

A. (5,﹣![]() )B. (8,1+
)B. (8,1+![]() )C. (11,﹣1﹣
)C. (11,﹣1﹣![]() )D. (14,1+
)D. (14,1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,∠B=90°,DC=5cm.点P从点A向点D以lcm/s的速度运动,到D点停止,点Q从点C向B点以2cm/s的速度运动,到B点停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;BQ= .
(2)当t为何值时,四边形PDCQ是平行四边形?
(3)当t为何值时,△QCD是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ).显然
).显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为![]() ,则称之为“生数”,比如
,则称之为“生数”,比如![]() 就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出
就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出![]() 个新的“生数”,比如由
个新的“生数”,比如由![]() 可以产生出
可以产生出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 个新“生数”,将这
个新“生数”,将这![]() 个数相加,得到的和
个数相加,得到的和![]() 称为由“生数”
称为由“生数”![]() 生成的“完全数”
生成的“完全数”
问题:(1)求证:任意一个“完全数”都可以整除![]() ;
;
(2)若一个四位正整数![]() (
(![]() ,
,![]() 是整数)是由一个“生数”
是整数)是由一个“生数”![]() (
(![]() ,
,![]() ,
, ![]() 、
、![]() 是整数)产生的“完全数”,请求出这个“生数”
是整数)产生的“完全数”,请求出这个“生数”![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
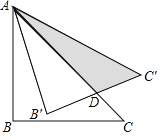
【题目】如图,等腰直角三角形ABC的直角边AB的长为![]() ,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com