
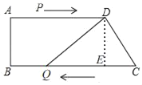
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,∠B=90°,DC=5cm.点P从点A向点D以lcm/s的速度运动,到D点停止,点Q从点C向B点以2cm/s的速度运动,到B点停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;BQ= .
(2)当t为何值时,四边形PDCQ是平行四边形?
(3)当t为何值时,△QCD是直角三角形?

【答案】(1)tcm,(15﹣2t)cm;(2)t=3秒;(3)当t为![]() 秒或
秒或![]() 秒时,△QCD是直角三角形.
秒时,△QCD是直角三角形.
【解析】
(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,BQ的长
(2)当AP=CQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当∠CDQ=90°或∠CQD=90°△QCD是直角三角形,分情况讨论t的一元一次方程方程,解方程求出符合题意的t值即可;
(1)由运动知,AP=t,CQ=2t,
∴BQ=BC﹣CQ=15﹣2t,
故答案为:tcm,(15﹣2t)cm;
(2)由运动知,AP=t,CQ=2t,
∴DP=AD﹣AP=12﹣t,
∵四边形PDCQ是平行四边形,
∴PD=CQ,
∴12﹣t=2t,
∴t=3秒;
(3)∵△QCD是直角三角形,
∴∠CDQ=90°或∠CQD=90°,
①当∠CQD=90°时,BQ=AD=12,
∴15﹣2t=12,
∴t=![]() 秒,
秒,
②当∠CDQ=90°时,如图,
过点D作DE⊥BC于E,
∴四边形ABED是矩形,
∴BE=AD=12,
∴CE=BC﹣BE=3,
∵∠CED=∠CDQ=90°,∠C=∠C,
∴△CDE∽△CQD,
∴![]() ,
,
∴![]() ,
,
∴t=![]() 秒,
秒,
即:当t为![]() 秒或
秒或![]() 秒时,△QCD是直角三角形.
秒时,△QCD是直角三角形.


科目:初中数学 来源: 题型:
【题目】一辆警车沿着一条南北方向的公路巡视,某天早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向北为正方向,当天行驶记录如下(单位:千米):
地,约定向北为正方向,当天行驶记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)问![]() 地在
地在![]() 地的哪个方向?相距多少千米?
地的哪个方向?相距多少千米?
(2)若警车出发时邮箱里剩油18升,该警车每小时耗油0.2升,请问警车在到达B地之前是否需要加油?若需要,至少加多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了![]() m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。
m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。

(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的北偏东多少度方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:

(1)菜地的长a=___米,宽b=___米;
(2)菜地的面积S=___平方米;
(3)求当x=1米时,菜地的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
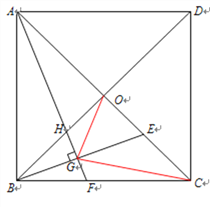
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
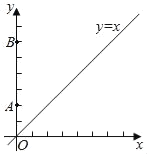
【题目】如图,在平面直角坐标系中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个边长为![]() 的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,
的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,

(1)用含有![]() 的代数式分别表示阴影面积:
的代数式分别表示阴影面积:![]() ,
,![]() ,
,![]() .
.
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,
,![]() ,求出图③中的阴影部分面积.
,求出图③中的阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com