
����Ŀ������ijר��������ijƷ�Ʒ�װ���÷�װ����Ϊÿ��80Ԫ����ÿ����װ�ۼ�Ϊ240Ԫʱ����������Ϊ200������ר����Ϊ��߾�Ӫ��������ȡ���۵ķ�ʽ���д��������г����鷢�֣������۵���ÿ����10Ԫ��������������20������ÿ����װ�ۼ�ΪxԪ����ר�������������Ϊy����
��1����y��x�Ĺ�ϵʽ��
��2����ij�½���ʱ����ר������������18000Ԫ���ۼ۶�Ϊ����Ԫ��ʹ������ﵽ33000Ԫ��
���𰸡���1��y����2x+680����2�����۵���Ӧ��Ϊ230Ԫ
��������
��1��ֱ��������������200+![]() ��20�õ�������ϵʽ��
��20�õ�������ϵʽ��
��2�����������������������۩��ɱ����г����̲����
�⣺��1��������ã�y��200+![]() ��20����2x+680��
��20����2x+680��
��2�������⣬��(x��80)(��2x+680)��33000
��������x2��420x+43700��0��
��(x��190)(x��230)��0��
x1��190��x2��230��
��x��190ʱ���ɱ���80��(680��2��190)��24000��18000������Ҫ����ȥ��
��x��230ʱ���ɱ���80��(680��2��230)��17600��18000����Ҫ��
�����۵���Ӧ��Ϊ230Ԫ��


 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ÿһ�������е�������ֵ�ֱ�Ϊ�����ε����߳�����3��4��5����6��8��10����5��12��13����![]() ��2��
��2��![]() �����в��ܹ���ֱ�������ε���____(�����)��
�����в��ܹ���ֱ�������ε���____(�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���⻪ũ������˾����50̨�����ո�������м���20̨������30̨���Ƚ���50̨�����ո������A��B�������ո�С������30̨����A������20̨����B���������������ũ������˾�̶���ÿ������۸������
ÿ̨�����ո������� | ÿ̨�����ո������� | |
A���� | 1800 | 1600 |
B���� | 1600 | 1200 |
��1��������A����x̨���������ո��������˾��50̨�����ո��һ���õ����Ϊy��Ԫ������y��x��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����ʹũ������˾��50̨�����ո��һ���õ�����ܶ����79 600Ԫ��˵���ж����ַ��䷽�����������ַ�����Ƴ�����
��3�����Ҫʹ��50̨�����ո��ÿ���õ������ߣ�����Ϊ�⻪ũ������˾��һ�����������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
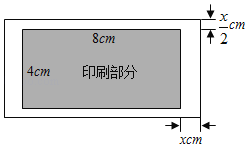
����Ŀ����ͼ��ӡˢһ�ž��εİ�װֽ��ӡˢ���ֵij�Ϊ8cm����Ϊ4cm�����¿հ���![]() cm�����ҿհ���xcm�����ܿհ״������ΪScm2��
cm�����ҿհ���xcm�����ܿհ״������ΪScm2��
��1����S��x�Ĺ�ϵʽ��
��2�������ܿհ״������Ϊ18cm2ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ʵ��![]() ��2��
��2��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �������·�ʽ����������
�������·�ʽ����������
![]() ��2��
��2��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��4
��4
����
�������Ĺ��ɼ������У�ֱ��![]() ��
��
����![]() ���ڵ�λ�������Ա�ʾΪ
���ڵ�λ�������Ա�ʾΪ![]() ��
��![]() ���ڵ�λ�������Ա�ʾΪ
���ڵ�λ�������Ա�ʾΪ![]() ���ش��������⣺
���ش��������⣺
��1��![]() ���ڵ�λ�������Ա�ʾΪ ��
���ڵ�λ�������Ա�ʾΪ ��
��2����ij����λ�������Ա�ʾΪ![]() ����������� ��
����������� ��
��3��![]() ���ڵ�λ�������Ա�ʾΪ ��
���ڵ�λ�������Ա�ʾΪ ��
��4������ʵ�����������������ڵ�λ�������Ա�ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�����ij�ֱ��䣬���ֱ���ÿ̨����Ϊ2500Ԫ����֪ԭ���ۼ�Ϊÿ̨2900Ԫʱ��ƽ��ÿ�����۳�8̨������ԭ���ۼ۵Ļ�����ÿ̨����50Ԫ����ƽ��ÿ��ɶ��۳�4̨����ÿ̨�����ʵ���ۼ۱�ԭ���ۼ۽�����xԪ��
��1����������軯��
ÿ���������/̨ | ÿ̨��������/Ԫ | |
����ǰ | 8 | 400 |
���ۺ� |
��2���̳�Ϊʹ���ֱ���ƽ��ÿ�����������ﵽ5000Ԫ����ÿ̨�����ʵ���ۼ�Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
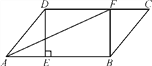
����Ŀ����ͼ������ABCD�У�����D��DE��AB�ڵ�E����F�ڱ�CD�ϣ�CF��AE������AF��BF.
��1����֤���ı���BFDE�Ǿ���
��2����CF��6��BF��8��DF��10����֤��AF�ǡ�DAB��ƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
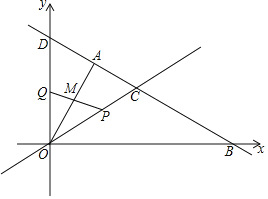
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB������A(![]() ��
��![]() )��B (2
)��B (2![]() ��0)������y�ύ�ڵ�D��ֱ��OC��AB���ڵ�C���ҵ�C�ĺ�����Ϊ
��0)������y�ύ�ڵ�D��ֱ��OC��AB���ڵ�C���ҵ�C�ĺ�����Ϊ![]() ��
��
(1)��ֱ��AB�Ľ���ʽ��
(2)����OA�����жϡ�AOD����״��
(3)����P�ӵ�C�������߶�CO��ÿ��1����λ���ȵ��ٶ����յ�O�˶����˶�ʱ��Ϊt�룬ͬʱ����Q�ӵ�O������y�������������ͬ���ٶ��˶�������Q�����Dʱ��P��Qͬʱֹͣ�˶�����PQ��OA���ڵ�M����tΪ��ֵʱ����OPMΪ���������Σ������������������tֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com