
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
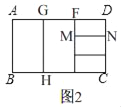
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
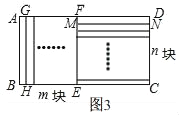
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

���𰸡���1��![]() ����2��
����2��![]() ����3��A����
����3��A����![]() ����
����![]() ��B����
��B����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
�������������������1���������ƱȵĶ�����⼴�ɣ���2���ɹ��ɶ������AB=5���������Ʊȵ���![]() ����ô𰸣���3��A.���ɾ���ABEF����FECD���г�����ʽ�����ɵã�����ÿ��С���ζ���ȫ�ȵģ��ɵ���߳�Ϊb��
����ô𰸣���3��A.���ɾ���ABEF����FECD���г�����ʽ�����ɵã�����ÿ��С���ζ���ȫ�ȵģ��ɵ���߳�Ϊb��![]() a���г�����ʽ�������ɣ�B.�ٷֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ��⣻���������֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�����DN=
a���г�����ʽ�������ɣ�B.�ٷֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ��⣻���������֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�����DN=![]() b��Ȼ��ֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ���.
b��Ȼ��ֵ�FM�Ǿ���DFMN�ij�ʱ�͵�DF�Ǿ���DFMN�ij�ʱ����������������ƶ���ε������б���ʽ���.
�⣺��1���ߵ�H��AD���е㣬
��AH=![]() AD��
AD��
��������AEOH��������ABCD��
�����Ʊ�Ϊ��![]() ==
==![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����Rt��ABC�У�AC=4��BC=3�����ݹ��ɶ����ã�AB=5��
���ACD���ABC���Ƶ����Ʊ�Ϊ��![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3��A���١߾���ABEF����FECD��
��AF��AB=AB��AD��
��![]() a��b=b��a��
a��b=b��a��
��a=![]() b��
b��
�ʴ�Ϊ��![]()
��ÿ��С���ζ���ȫ�ȵģ�����߳�Ϊb��![]() a��
a��
��b��![]() a=a��b��
a=a��b��
��a=![]() b��
b��
�ʴ�Ϊ��![]()
B������ͼ2��
�ɢ٢ڿ�֪����2�����ȫ�ȣ�����3�����Ҳȫ�ȣ�
��DN=![]() b��
b��
������FM�Ǿ���DFMN�ij�ʱ��
�߾���FMND����ABCD��
��FD��DN=AD��AB��
��FD��![]() b=a��b��
b=a��b��
���FD=![]() a��
a��
��AF=a��![]() a=
a=![]() a��
a��
��AG=![]() =
=![]() =
=![]() a��
a��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() a��b=b��a
a��b=b��a
�ã�a=![]() b��
b��
������DF�Ǿ���DFMN�ij�ʱ��
�߾���DFMN����ABCD��
��FD��DN=AB��AD
��FD��![]() b=b��a
b=b��a
���FD=![]() ��
��
��AF=a��![]() =
=![]() ��
��
��AG=![]() =
=![]() ��
��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() ��b=b��a��
��b=b��a��
�ã�a=![]() b��
b��
�ʴ�Ϊ��![]() ��
��![]() ��
��
����ͼ3��
�ɢ٢ڿ�֪����m�����ȫ�ȣ�����n�����Ҳȫ�ȣ�
��DN=![]() b��
b��
������FM�Ǿ���DFMN�ij�ʱ��
�߾���FMND����ABCD��
��FD��DN=AD��AB��
��FD��![]() b=a��b��
b=a��b��
���FD=![]() a��
a��
��AF=a��![]() a��
a��
��AG=![]() =
=![]() =
=![]() a��
a��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() a��b=b��a
a��b=b��a
�ã�a=![]() b��
b��
������DF�Ǿ���DFMN�ij�ʱ��
�߾���DFMN����ABCD��
��FD��DN=AB��AD
��FD��![]() b=b��a
b=b��a
���FD=![]() ��
��
��AF=a��![]() ��
��
��AG=![]() =
=![]() ��
��
�߾���GABH����ABCD��
��AG��AB=AB��AD
��![]() ��b=b��a��
��b=b��a��
�ã�a=![]() b��
b��
�ʴ�Ϊ��![]() b��
b��![]() b��
b��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�����оٰ�������������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 6 |
��2�� | 30��x��35 | 8 |
��3�� | 35��x��40 | 16 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |

����ͼ��������и��⣺
��1�������a��ֵ����2�����Ƶ���ֲ�ֱ��ͼ����������
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
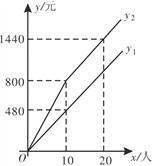
����Ŀ��ij������Ʊ���涨���ǽڼ��յ�Ʊ�۴�a����Ʊ���ڼ��ո����Ŷ�����x(��)ʵ�зֶ���Ʊ����![]() 10����ԭչ�۹�����x>10��������10�˰�ԭƱ�۹��������ֵİ�ԭ�Ǽ۴�b�۹���ij��������ŵ��þ������������ڷǽڼ��յĹ�Ʊ��Ϊy1Ԫ���ڽڼ��յĹ�Ʊ��Ϊy2Ԫ��y1��y2��x֮��ĺ���ͼ����ͼ��ʾ��
10����ԭչ�۹�����x>10��������10�˰�ԭƱ�۹��������ֵİ�ԭ�Ǽ۴�b�۹���ij��������ŵ��þ������������ڷǽڼ��յĹ�Ʊ��Ϊy1Ԫ���ڽڼ��յĹ�Ʊ��Ϊy2Ԫ��y1��y2��x֮��ĺ���ͼ����ͼ��ʾ��
(1)�۲�ͼ���֪��a=________��b=________��
(2)��x>10ʱ����y2��x֮��ĺ�������ʽ��
(3)���������ڽ���5��1Ŀ��������5��10��(�ǽڼ���)���ҹ����þ������������źϼ�50�ˣ�������Ʊ��3120Ԫ����֪������������10�ˣ����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���������֭���Ϻ�̼�����Ϲ�60�䣬��������ÿ��Ľ��ۺ��ۼ����±���ʾ���蹺����֭����x�䣨xΪ������������������������������ȫ����������õ�������ΪWԪ��ע�����������ۼۣ��ܽ��ۣ���
��1�����̳�����̼������y�䣬ֱ��д��y��x�ĺ�������ʽ��
��2����������w����x�ĺ�������ʽ��
��3����������������ϵ��ܷ��ò�����2100Ԫ����ô���̳���ν������ܻ�����ࣿ������������
���� | ��֭���� | ̼������ |
���ۣ�Ԫ/�䣩 | 40 | 25 |
�ۼۣ�Ԫ/�䣩 | 52 | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�У�AB=10��AD=8����E��BC����һ�����㣬����ABE��AE�۵��õ���AB��E��
��1����ͼ(1)����G�͵�H�ֱ���AD��AB����е㣬����B���ڱ�DC�ϡ�
����GH�ij���
����֤����AGH�ա�B��CE��
��2����ͼ(2)������F��AE���е㣬����B��F��B��F��AD����DC��I��
����֤���ı���BEB��F�����Σ�
����B��F�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b������������a��b��ţ��ԱȽ�|a+b|��|a��b|��|a|+|b|�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵ�������м�������15�ˣ�������Ϊ�˺����ƶ���Ʒ��ÿ���������ͳ������15��ij�µļӹ����������
ÿ�˼ӹ�������� | 540 | 450 | 300 | 240 | 210 | 120 |
���� | 1 | 1 | 2 | 6 | 3 | 2 |
(1)д����15�˸��¼ӹ��������ƽ��������λ����������
(2)���������������˰�ÿλ���˵��¼ӹ����������Ϊ260������Ϊ��������Ƿ������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�����ԭ��![]() ������������.����.����.���ҵķ�������ƽ�ƣ�ÿ���ƶ�һ����λ���õ�
������������.����.����.���ҵķ�������ƽ�ƣ�ÿ���ƶ�һ����λ���õ�![]() ��0��1����
��0��1����![]() ��1��1����
��1��1����![]() ��1��0����
��1��0����![]() ��2��0��������ô��
��2��0��������ô��![]() ������Ϊ__________.
������Ϊ__________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com