
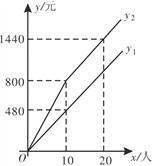
����Ŀ��ij������Ʊ���涨���ǽڼ��յ�Ʊ�۴�a����Ʊ���ڼ��ո����Ŷ�����x(��)ʵ�зֶ���Ʊ����![]() 10����ԭչ�۹�����x>10��������10�˰�ԭƱ�۹��������ֵİ�ԭ�Ǽ۴�b�۹���ij��������ŵ��þ������������ڷǽڼ��յĹ�Ʊ��Ϊy1Ԫ���ڽڼ��յĹ�Ʊ��Ϊy2Ԫ��y1��y2��x֮��ĺ���ͼ����ͼ��ʾ��
10����ԭչ�۹�����x>10��������10�˰�ԭƱ�۹��������ֵİ�ԭ�Ǽ۴�b�۹���ij��������ŵ��þ������������ڷǽڼ��յĹ�Ʊ��Ϊy1Ԫ���ڽڼ��յĹ�Ʊ��Ϊy2Ԫ��y1��y2��x֮��ĺ���ͼ����ͼ��ʾ��
(1)�۲�ͼ���֪��a=________��b=________��
(2)��x>10ʱ����y2��x֮��ĺ�������ʽ��
(3)���������ڽ���5��1Ŀ��������5��10��(�ǽڼ���)���ҹ����þ������������źϼ�50�ˣ�������Ʊ��3120Ԫ����֪������������10�ˣ����������������������
���𰸡�(1) 6,8��(2) y2=64x+160 (x��10) ;(3) ������35�ˣ�������15��.
����������������1���ɺ���ͼ���ù�Ʊ�������Զ��۵Ŀ������ó�a��ֵ���õ�11�˵�20�˵Ĺ�Ʊ�������Զ��۵Ŀ������ó�b��ֵ��
��2�����ô���ϵ��������������������ʽ���y2��x�ĺ�����ϵʽ���ɣ�
��3����A����n�ˣ���ʾ��B�ŵ�����Ϊ��50-n����Ȼ����ݣ�2���ĺ�����ϵʽ�г�������⼴�ɣ�
��⣺��1����y1ͼ���ϵ㣨10��480�����õ�10�˵ķ���Ϊ480Ԫ��
��a=![]() ��10=6��
��10=6��
��y2ͼ���ϵ㣨10��800���ͣ�20��1440�����õ�20���к�10�˷���Ϊ640Ԫ��
��b=![]() ��10=8��
��10=8��
�ʴ�Ϊ6��8��
��2����x��10ʱ����y2=kx+b.
��ͼ����㣨10,800������20,1440��,
��![]()
���![]()
��y2=64x+160 (x��10) .
��3���������m�ˣ�������n��.
��ͼ��y1=48x.
��m��10ʱ��
�����⣬��![]()
���![]()
�𣺼�����35�ˣ�������15��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ���ŵĽ������������״�����������˵���ˮ��ľ��붼��1m�����ŵĿ��Ϊ10m��������ˮ�����������5m���Ŷ�������ϸ���һյ����ˮ��4m���۵ƣ�
��1���������ߵĽ���ʽ��
��2������յ���۵�֮���ˮƽ���룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ����ϣ�������⣮
��n��һ����λ��������λ�ϵ����ֻ�����ͬ���Ҷ���Ϊ�㣬��������λ�ϵ���������ѡ��������һ����λ���������Ϳ��Եõ�������ͬ����λ�������ǰ���������ͬ����λ��������n�ġ�������������n�����С���������֮����22���̼�ΪG��n��������n=123����������������������12��13��21��23��31��32�������������������ĺ�12+13+21+23+31+32=132��132��22=6������G��123��=6��
��1�����㣺G��125����G��746����
��2����s��t��������λ�������Ƕ��С�����������a��1��4�ֱ���s�İ�λ��ʮλ����λ�ϵ����֣�x��y��6�ֱ���t�İ�λ��ʮλ����λ�ϵ����֣��涨��k=![]() ����G��s��G��t��=84����k����Сֵ��
����G��s��G��t��=84����k����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
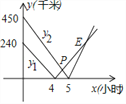
����Ŀ����һ����ֱ�ĸ��ٹ�·��������3����־��A��B��C���ס��������ֱ��A��C����ͬʱ������������ʻ���׳���A��B��C���ҳ���C��B��A���ס���������B�ľ���y1��y2��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵͼ����ͼ��ʾ���۲�ͼ�������н��ۣ���A��C֮���·��Ϊ690ǧ�ף����ҳ��ȼ׳�ÿСʱ��30ǧ�ף���4.5Сʱ�����������ܵ�E�ĺ������ʾ�����ڶ���������ʱ�䣻�ݵ�E������Ϊ��7��180��������ȷ����________����������ȷ���۵���Ŷ����ں����ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ������Ӫ��У�С����Ӫ��A�������ر�ƫ��60�㷽������![]() m �����B��Ȼ�����ر�ƫ��30�㷽������50m����Ŀ�ĵ�C��
m �����B��Ȼ�����ر�ƫ��30�㷽������50m����Ŀ�ĵ�C��

��1����A��C����֮��ľ��룻
��2��ȷ��Ŀ�ĵ�C��Ӫ��A�ı�ƫ�����ٶȷ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУѧ����ѧ�ڲμ�������������ѧУ��������˱�У50��ѧ���μ�������Ĵ����������������õ������������£�
�����x | Ƶ�� | Ƶ�� |
0<x��3 | 10 | 0.20 |
3<x��6 | a | 0.24 |
6<x��9 | 16 | 0.32 |
9<x��12 | m | b |
12<x��15 | 4 | 0.08 |
15<x��18 | 2 | n |

��������ͼ����Ϣ������������⣺
��1������a=___��b=___��
��2�����Ƶ���ֲ�ֱ��ͼ������������ͼ�����ע��Ӧ�����ݣ���
��3������У����1500��ѧ��������Ƹ�У����ѧ�ڲμ����������6�ε�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
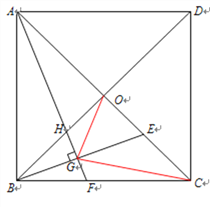
����Ŀ����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��EΪOC�϶���(���O���غ�)����AF��BE������ΪG����BC��F����B0��H������OG��CC��
(1)��֤��AH=BE��
(2)��̽������AGO�Ķ����Ƿ�Ϊ��ֵ?��˵�����ɣ�
(3)��OG��CG��BG=![]() ������OGC�������
������OGC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������裬����Ժ������ȫ��ʵʩ���ҵ�����������. ��һ������ҵ�����IJ�ƷΪ�ʵ硢���䡢ϴ�»����ֻ����ֲ�Ʒ. ij��һ�Ҽҵ��̳���ȥ���һ���ȶ��������ֲ�Ʒ���������������ͳ�ƣ����������µ�ͳ��ͼ���������ͼ����Ϣ����������⣺

��1�����̳���һ����һ��������_________̨�ҵ磻
��2���벹ȫ����ͳ��ͼ�����������ͳ��ͼ�вʵ����ڵ�����Բ�ĽǵĶ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com