
【题目】如图,在平行四边形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() ,且两个顶点
,且两个顶点![]() 、
、![]() 分别在
分别在![]() 轴,
轴,![]() 轴上滑动,连接
轴上滑动,连接![]() ,则
,则![]() 的最小值是______.
的最小值是______.
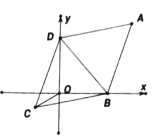
【答案】10![]() 10.
10.
【解析】
由条件可先证得△CBD是等边三角形,过点C作CE⊥BD于点E,当点C,O,E在一条直线上,此时CO最短,可求得OE和CE的长,进而得出OC的最小值.
如图所示:过点C作CE⊥BD于点E,
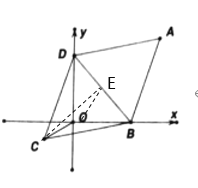
∵![]() 是等边三角形,
是等边三角形,
∴AB=BD=AD=20,∠BAD=60°,
∵平行四边形ABCD中,AB=CD,BC=AD,∠BAD=∠BCD=60°,
∴CD=BC=BD=20,
∴△CBD是等边三角形,∠CBD=60°,
∵CE⊥BD,△CBD是等边三角形,
∴E为BD中点,
∵∠DOB=90°,E为BD中点,
∴![]() ,
,

当点C,O,E在一条直线上,此时OC最短,
故CO的最小值为:CO=CEEO= CB·sin∠CBE-10=CB·sin60°-10=10![]() 10,
10,
故答案为:10![]() 10.
10.


科目:初中数学 来源: 题型:
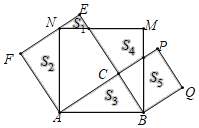
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把能被13整除的数称为“自觉数”,已知一个整数,把其个位数字去掉,再从余下的数中加上个位数的4倍如果和是13的倍数,则原数为“自觉数”,如果数字仍然太大不能直接观察出来就重复此过程.如416:41+4×6=65,65÷13=5,所以416是自觉数;又如25281:2528+4×1=2532,253+4×2=261,26+4×1=30,因为30不能被13整除,所以25281不是“自觉数”.
(1)判断27365是否为自觉数 (填“是”或者“否”).
(2)一个四位数n=![]() ,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
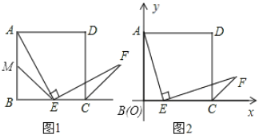
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
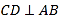
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com