
【题目】我们把能被13整除的数称为“自觉数”,已知一个整数,把其个位数字去掉,再从余下的数中加上个位数的4倍如果和是13的倍数,则原数为“自觉数”,如果数字仍然太大不能直接观察出来就重复此过程.如416:41+4×6=65,65÷13=5,所以416是自觉数;又如25281:2528+4×1=2532,253+4×2=261,26+4×1=30,因为30不能被13整除,所以25281不是“自觉数”.
(1)判断27365是否为自觉数 (填“是”或者“否”).
(2)一个四位数n=![]() ,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
【答案】(1)是;(2)32.
【解析】
(1)根据“自觉数”的方法计算即可得出结论;
(2)先确定出n既能被5整除也能被13整除,进而确定出![]() 或
或![]() ,分两种情况,利用n能13整除计算即可得出结论.
,分两种情况,利用n能13整除计算即可得出结论.
(1)![]()
![]()
![]()
因为65能被13整除
所以27365是自觉数
故答案为:是;
(2)∵四位数![]() 能被65整除
能被65整除
∴四位数![]() 既能被13整除也能被5整除
既能被13整除也能被5整除
∵四位数n能被5整除
∴四位数n的个位数字是0或5
即![]() 或
或![]()
∵四位数n的千位数字和十位数字相同
![]()
当![]() 时,
时,![]()
去掉个位数字0,得到三位数![]()
∵四位数![]() 能被13整除
能被13整除
∴三位数![]() 能被13整除
能被13整除
再去掉个位数字a,得到两位数![]()
则![]() 能被13整除
能被13整除
∵b是四位数字的百位数字
![]()
![]()
![]()
![]() 或39或52或65
或39或52或65
当![]() 时,
时,![]() ,不存在符合题意的a,b的值
,不存在符合题意的a,b的值
当![]() 时,
时,![]() ,不存在符合题意的a,b的值
,不存在符合题意的a,b的值
当![]() 时,
时,![]() ,不存在符合题意的a,b的值
,不存在符合题意的a,b的值
当![]() 是,
是,![]() ,此时
,此时![]()
即![]()
![]()
当![]() 时,
时,![]()
去掉个位数字5得到三位数![]()
∵四位数![]() 能被13整除
能被13整除
![]() 能被13整除
能被13整除
而![]() 的个位数字是a
的个位数字是a
再去掉个位数字,得到的两位数的个位数字为![]() ,十位数字是a
,十位数字是a
则![]() 能被13整除
能被13整除
![]()
![]()
![]() 或39或52或65
或39或52或65
当![]() 时,
时,![]() ,不存在符合题意的a,b的值
,不存在符合题意的a,b的值
当![]() 时,
时,![]() ,此时
,此时![]()
即![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]()
即![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]()
即![]()
![]()
综上,![]() 的值为32或11或16或19
的值为32或11或16或19
故![]() 最大值为32.
最大值为32.


科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
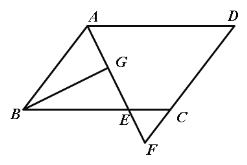
【题目】如图,在![]() ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=![]() ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
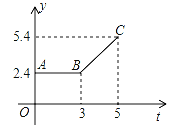
【题目】图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图象.
(1)从图象知,通话2分钟需付的电话费是 元;
(2)当t≥3时求出该图象的解析式(写出求解过程);
(3)通话7分钟需付的电话费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
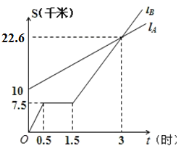
【题目】如图![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() 与
与![]() 时间的关系,根据图象回答下列问题:
时间的关系,根据图象回答下列问题:
(1)![]() 出发时与
出发时与![]() 相距 千米;
相距 千米;
(2)走了一段路后,![]() 自行车发生故障,进行修理,所用的时间是 小时;
自行车发生故障,进行修理,所用的时间是 小时;
(3)![]() 出发后 小时与
出发后 小时与![]() 相遇;
相遇;
(4)求![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
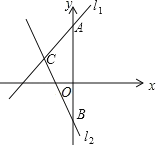
【题目】如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1相交于C(﹣3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com