
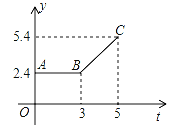
【题目】图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图象.
(1)从图象知,通话2分钟需付的电话费是 元;
(2)当t≥3时求出该图象的解析式(写出求解过程);
(3)通话7分钟需付的电话费是多少元?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A.![]() =
=![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把能被13整除的数称为“自觉数”,已知一个整数,把其个位数字去掉,再从余下的数中加上个位数的4倍如果和是13的倍数,则原数为“自觉数”,如果数字仍然太大不能直接观察出来就重复此过程.如416:41+4×6=65,65÷13=5,所以416是自觉数;又如25281:2528+4×1=2532,253+4×2=261,26+4×1=30,因为30不能被13整除,所以25281不是“自觉数”.
(1)判断27365是否为自觉数 (填“是”或者“否”).
(2)一个四位数n=![]() ,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
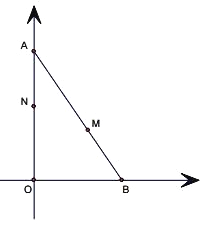
【题目】如图,己知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
(1)当t为何值时,M为AB的中点;
(2)当t为何值时,△AMN为直角三角形;
(3)当t为何值时,△AMN是等腰三角形?并求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
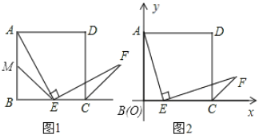
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 ![]() +
+ ![]() =2的解为正数,且不等式组
=2的解为正数,且不等式组 ![]() 无解的概率是________.
无解的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com