
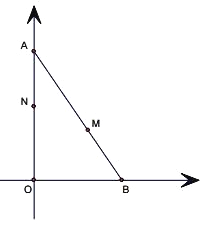
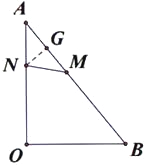
【题目】如图,己知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
(1)当t为何值时,M为AB的中点;
(2)当t为何值时,△AMN为直角三角形;
(3)当t为何值时,△AMN是等腰三角形?并求此时点M的坐标.
【答案】(1)当t=![]() 秒时,M是AB的中点;(2)当
秒时,M是AB的中点;(2)当![]() 或
或![]() 时,△AMN为直角三角形;
时,△AMN为直角三角形;
(3)当![]() ,
,![]() ,
, ![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由勾股定理求出AB的长,再由中点的定义即可得出结论;
(2)运动t秒时,AN=t,BM=2t,AM=10-2t.然后分两种情况讨论:①当MN⊥AO时,△ANM∽△AOB;②当MN⊥AB时,△ANM∽△ABO;
(3)先求出M的坐标,然后分三种情况讨论:①AM=AN;②MA=MN;③NA=NM.
(1)∵A(0,8),B(6,0),∴OA=8,OB=6,∴AB=10.
∵M为AB的中点,∴MB=2t=5,∴t=![]() .
.
答:当t=![]() 秒时,M是AB的中点.
秒时,M是AB的中点.
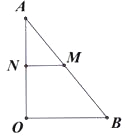
(2)运动t秒时,AN=t,BM=2t,AM=10-2t.
①当MN⊥AO时,△ANM∽△AOB,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
②当MN⊥AB时,△ANM∽△ABO,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() .
.
综上:当 t=![]() 或 t=
或 t=![]() 时,△AMN为直角三角形.
时,△AMN为直角三角形.
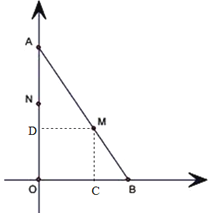
(3)如图,过M作MC⊥OB于C,MD⊥OA于D.
∵AO⊥OB,∴∠MCB=∠AOB.
∵∠MBC=∠ABO,∴△MBC∽△ABO,∴![]() ,∴
,∴![]() ,∴MC=
,∴MC=![]() ,CB=
,CB=![]() ,∴OC=
,∴OC=![]() ,∴M(
,∴M(![]() ,
,![]() ).分三种情况讨论:
).分三种情况讨论:
①当AM=AN时,t=102t,解得:![]() ,∴M(2,
,∴M(2,![]() );
);

②当MA=MN时,过M作MF⊥AO,交AO于F,如图:
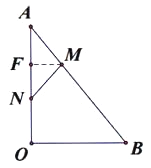
则F是AN的中点,AF=![]() ,这时,△AFM∽△AOB,∴
,这时,△AFM∽△AOB,∴![]() ,∴
,∴![]() ,解得
,解得 ![]() ,∴M(
,∴M(![]() ,
,![]() );
);
③当NA=NM时,过N作NG⊥AB,交AB于G,如图,则G是AM的中点,AG=5t.
这时,△AGN∽△AOB,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴M(
,∴M(![]() ,
,![]() ).
).
综上,当 ![]() 或
或![]() 或
或![]() 时,△AMN为等腰三角形,此时,M点的坐标分别是
时,△AMN为等腰三角形,此时,M点的坐标分别是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
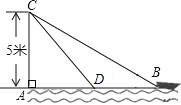
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
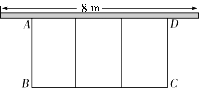
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点M(4,0)为圆心,MO为半径的半圆交x轴于点A,P为半圆上的一个动点,以点P为直角顶点在OP上方作Rt△OPB,且OP=2PB,OB交半圆于点Q.

(1)当P为半圆弧的中点时,求△OPB的面积.
(2)在运动过程中,求MB的最大值.
(3)在运动过程中,若点Q将线段OB分为1:2的两部分,求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com