
【题目】已知![]() 和
和![]() 是两个等腰直角三角形,
是两个等腰直角三角形,![]() .连接
.连接![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.

(1)如图![]() ,当
,当![]() 与
与![]() 在同一直线上时,求证:
在同一直线上时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)证明见详解;
(2)证明见详解
【解析】
(1)如图所示,延长BM交EF于点D,延长AB交CF于点H,证明为△BED是等腰直角三角形和M是BD的中点即可求证结论;
(2)如图所示,做辅助线,推出BM、ME是中位线进而求证结论.
证明(1)如图所示,延长BM交EF于点D,延长AB交CF于点H
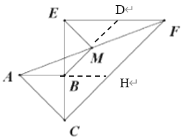
易知:△ABC和△BCH均为等腰直角三角形
∴AB=BC=BH
∴点B为线段AH的中点
又∵点M是线段AF的中点
∴BM是△AHF的中位线
∴BM∥HF
即BD∥CF
∴∠EDM=∠EFC=45°
∠EBM=∠ECF=45°
∴△EBD是等腰直角三角形
∵∠ABC=∠CEF=90°
∴AB∥EF
∴∠BAM=∠DFM
又M是AF的中点
∴AM=FM
在△ABM和△FDM中
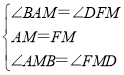
∴△ABM≌△FDM(ASA)
∴BM=DM,M是BD的中点
∴EM是△EBD斜边上的高
∴EM⊥BM
(2)如图所示,延长AB交CE于点D,连接DF,易知△ABC和△BCD均为等腰直角三角形
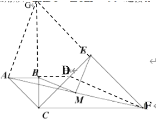
∴AB=BC=BD,AC=CD
∴点B是AD的中点,
又∵点M是AF的中点
∴BM=![]() DF
DF
延长FE交CB于点G,连接AG,易知△CEF和△CEG均为等腰直角三角形
∴CE=EF=EG,CF=CG
∴点E是FG的中点,
又∵点M是AF的中点
∴ME=![]() AG
AG
在△ACG与△DCF中,
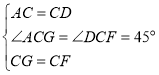
∴△ACG≌△DCF(SAS)
∴DF=AG
∴BM=ME


科目:初中数学 来源: 题型:
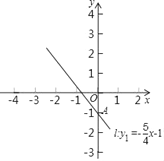
【题目】如图,直线l:y1=﹣![]() x﹣1与y轴交于点A,一次函数y2=
x﹣1与y轴交于点A,一次函数y2=![]() x+3图象与y轴交于点B,与直线l交于点C.
x+3图象与y轴交于点B,与直线l交于点C.
(1)画出一次函数y2=![]() x+3的图象;
x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
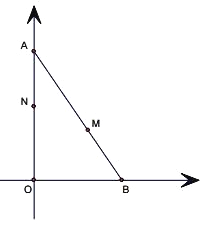
【题目】如图,己知A(0,8),B(6,0),点M、N分别是线段AB、AO上的动点,点M从点B出发,以每秒2个单位的速度向点A运动,点N从点A出发,以每秒1个单位的速度向点O运动,点M、N中有一个点停止时,另一个点也停止。设运动时间为t秒。
(1)当t为何值时,M为AB的中点;
(2)当t为何值时,△AMN为直角三角形;
(3)当t为何值时,△AMN是等腰三角形?并求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
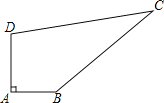
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,点 A( 2,2)、B(0,1)点 P 在 x 轴上,且△PAB 的等腰三角形,则满足条件的点 P 共有()个
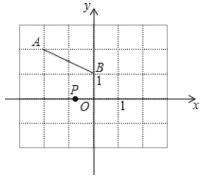
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 是射线
是射线![]() 上任意点(点
上任意点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() .
.

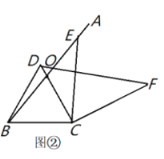
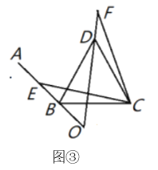
(1)如图①,猜想![]() 的度数是__________;
的度数是__________;
(2)如图②,图③,当![]() 是锐角或钝角时,其他条件不变,猜想
是锐角或钝角时,其他条件不变,猜想![]() 的度数,并选取其中一种情况进行证明;
的度数,并选取其中一种情况进行证明;
(3)如图③,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是中线,延长
是中线,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,下面给出的四个结论:①
,下面给出的四个结论:①![]() ,②
,②![]() 平分
平分![]() ,③
,③![]() ,④
,④![]() ,其中正确的个数是( )
,其中正确的个数是( )
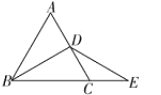
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com