
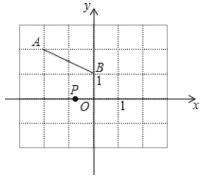
【题目】如图,直角坐标系中,点 A( 2,2)、B(0,1)点 P 在 x 轴上,且△PAB 的等腰三角形,则满足条件的点 P 共有()个
A.1B.2C.3D.4
【答案】D
【解析】
由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
如图,点A(-2,2)、B(0,1),

①以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=-![]() ,
,
∴P4(-![]() ,0).
,0).
∴符合条件的点有4个.
故选:D.


科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点M(4,0)为圆心,MO为半径的半圆交x轴于点A,P为半圆上的一个动点,以点P为直角顶点在OP上方作Rt△OPB,且OP=2PB,OB交半圆于点Q.

(1)当P为半圆弧的中点时,求△OPB的面积.
(2)在运动过程中,求MB的最大值.
(3)在运动过程中,若点Q将线段OB分为1:2的两部分,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
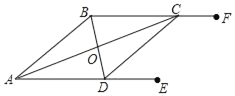
【题目】如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本65页有这样一道习题:
如图1,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1)△ACD与△CBD相似吗?为什么?
(2)图中还有几对相似三角形?是哪几对?
复习时,小明提出了新的发现:“利用△ACD∽△CBD∽△ABC可以进一步证明:
①CD2=ADBD,②BC2=BDAB,③AC2=ADAB.”
(1)请你按照小明的思路,选择①、②、③中的一个进行证明;
(2)小亮研究“小明的发现”时,又惊喜地发现,利用“它”可以证明“勾股定理”,请你按照小亮思路完成这个证明;
(3)小丽也由小明发现的“CD2=ADBD”,进一步发现:“已知线段a、b,可以用尺规作图作出线段c,使c2=ab”,请你完成小丽的发现.(不要求写出作法,请保留作图痕迹)
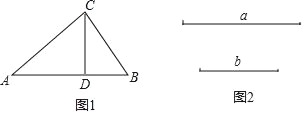
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com