
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

【答案】(1)300米/分;(2)y=﹣300x+3000;(3)![]() 分.
分.
【解析】
(1)由图象看出所需时间.再根据路程÷时间=速度算出小张骑自行车的速度.
(2)根据由小张的速度可知:B(10,0),设出一次函数解析式,用待定系数法求解即可.
(3)求出CD的解析式,列出方程,求解即可.
解:(1)由题意得:![]() (米/分),
(米/分),
答:小张骑自行车的速度是300米/分;
(2)由小张的速度可知:B(10,0),
设直线AB的解析式为:y=kx+b,
把A(6,1200)和B(10,0)代入得:![]()
解得:![]()
∴小张停留后再出发时y与x之间的函数表达式;![]()
(3)小李骑摩托车所用的时间: ![]()
∵C(6,0),D(9,2400),
同理得:CD的解析式为:y=800x﹣4800,
则![]()
![]()
答:小张与小李相遇时x的值是![]() 分.
分.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).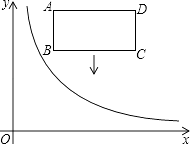
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
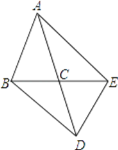
【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校初中学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查.在确定调查对象时,大家提出以下几种方案:A.对各班班长进行调查;B.对某班的全体学生进行调查;C.从全校每班随机抽取5名学生进行调查.在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会将收集到的数据整理后绘制成如图所示的条形统计图.
(1)为了使收集到的数据具有代表性.学生会在确定调查对象时应选择方案________ (填A,B或C);
(2)被调查的学生每天做作业所用时间的众数为________h;
(3)根据以上统计结果,估计该校900名初中学生中每天做作业用1.5 h的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寿县教育部门计划在3月12日植树节当天安排![]() ,
,![]() 两校部分学生到森林公园参加植树活动.已知
两校部分学生到森林公园参加植树活动.已知![]() 校区的每位学生往返车费是6元,
校区的每位学生往返车费是6元,![]() 校每位学生的往返车费是10元,要求两所学校均要有学生参加,且
校每位学生的往返车费是10元,要求两所学校均要有学生参加,且![]() 校参加活动的学生比
校参加活动的学生比![]() 校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求
校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求![]() ,
,![]() 两校最多各有多少学生参加?
两校最多各有多少学生参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州地铁5号线全长48.18公里,投资315.9亿元,规划建设预期2014-2019年,杭州工程地铁队负责建设,分两个班组分别从杭州南站外香樟路站和余杭科技岛站同时开工掘进.已知甲组比乙组平均每天多掘进2.4米,经过5天施工,两组共掘进了110米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进1.7米,乙组平均每天能比原来多掘进1.3米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
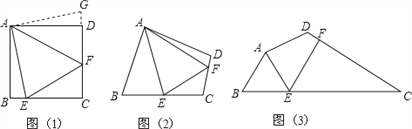
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com