
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A.![]() =
=![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
【答案】A.
【解析】
试题分析:已知∠B=∠C=36°,可得AB=AC,∠BAC=108°,又因DH垂直平分AB,EG垂直平分AC,根据中垂线性质得DB=DA,EA=EC,所以∠B=∠DAB=∠C=∠CAE=36°,即可判定△BDA∽△BAC,根据相似三角形的性质可得![]() =
=![]() ,再由∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,所以∠ADC=∠DAC,即可得CD=CA=BA,即BD=BC﹣CD=BC﹣AB,所以
,再由∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,所以∠ADC=∠DAC,即可得CD=CA=BA,即BD=BC﹣CD=BC﹣AB,所以![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,选项A错误;因为∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,所以∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,即可得AD,AE将∠BAC三等分,选项B正确;因为∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,可得∠BAE=∠CAD,在△BAE和△CAD中,
,选项A错误;因为∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,所以∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,即可得AD,AE将∠BAC三等分,选项B正确;因为∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,可得∠BAE=∠CAD,在△BAE和△CAD中, ,所以△BAE≌△CAD,选项C正确;由△BAE≌△CAD可得S△BAE=S△CAD,S△BAD+S△ADE=S△CAE+S△ADE,所以S△BAD=S△CAE,又因DH垂直平分AB,EG垂直平分AC,所以S△ADH=
,所以△BAE≌△CAD,选项C正确;由△BAE≌△CAD可得S△BAE=S△CAD,S△BAD+S△ADE=S△CAE+S△ADE,所以S△BAD=S△CAE,又因DH垂直平分AB,EG垂直平分AC,所以S△ADH=![]() S△ABD,S△CEG=
S△ABD,S△CEG=![]() S△CAE,即S△ADH=S△CEG,选项D正确.故答案选A.
S△CAE,即S△ADH=S△CEG,选项D正确.故答案选A.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】希望中学为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红和小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元,且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)为了奖励更多的同学,学校决定再次购进甲、乙两种笔记本,若买甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购买这两种笔记本的总金额不超过320元,求这次购买乙种笔记本最多多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF、EC,且CF=EF,下列结论正确的个数是( )
①CF平分∠BCD;②∠EFC=2∠CFD;③∠ECD=90°;④CE⊥AB.
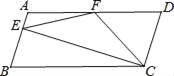
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=![]() ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
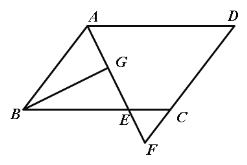
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
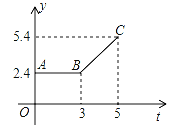
【题目】图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图象.
(1)从图象知,通话2分钟需付的电话费是 元;
(2)当t≥3时求出该图象的解析式(写出求解过程);
(3)通话7分钟需付的电话费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com