
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
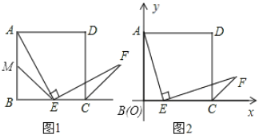
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
【答案】(1)证明见解析;(2) AE=EF一定成立,理由见解析;②F点坐标为![]()
【解析】
(1)利用ASA证明△AME≌△ECF,可得结论;
(2) ①在AB上截取AM=EC,连接ME,同(1)证明△AME≌△ECF,可得AE=EF;
②设F (a,-2a+6),过F作FH⊥x轴于H,作FG⊥CD于G,则可用a表示出FG、FH,由角平分线的性质得到关于a的方程,求得a的值,即可得出F的坐标.
(1)证明:∵∠BAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
∵M、E为中点,
∴AM=EC=BE=BM,
∴∠BME=45°,
∵CF平分∠DCB,
∴∠AME=∠ECF=135°,
在△AME和△ECF中, ,
,
∴△AME≌△ECF (ASA) ,
∴AE=EF;
(2)解:①若点E在线段BC上滑动时AE=EF一定成立.
证明:如图2中,在AB上截取AM=EC,连接ME,
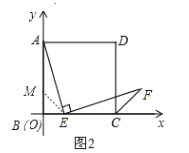
∵AB=BC,
∴BM=BE,
∴△MBE是等腰直角三角形,
∴∠AME=180°-45°=135°,
又∵CF是角平分线,
∴∠ECF=90°+45°=135°,
∴∠AME=∠ECF,
∵∠BAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
在△AME和△ECF中, ,
,
∴△AME≌△ECF (ASA) ,
∴AE=EF;
②设F (a,-2a+6),过F作FH⊥x轴于H,作FG⊥CD于G,如图3,
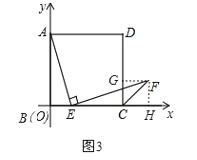
则FG=CH=a-1,FH=-2a+6,
∵CF为角平分线,
∴FH=FG,
∴a-1=-2a+6,
解得![]() ,
,
当![]() 时,
时,![]() ,
,
∴F点坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场花9万元从厂家购买A型和B型两种型号的电视机共50台,其中A型电视机的进价为每台1500元,B型电视机的进价为每台2500元.
(1)求该商场购买A型和B型电视机各多少台?
(2)若商场A型电视机的售价为每台1700元,B型电视机的售价为每台2800元,不考虑其他因素,那么销售完这50台电视机该商场可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
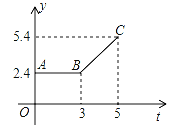
【题目】图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图象.
(1)从图象知,通话2分钟需付的电话费是 元;
(2)当t≥3时求出该图象的解析式(写出求解过程);
(3)通话7分钟需付的电话费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
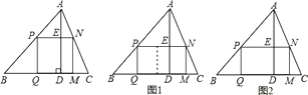
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
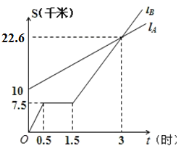
【题目】如图![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() 与
与![]() 时间的关系,根据图象回答下列问题:
时间的关系,根据图象回答下列问题:
(1)![]() 出发时与
出发时与![]() 相距 千米;
相距 千米;
(2)走了一段路后,![]() 自行车发生故障,进行修理,所用的时间是 小时;
自行车发生故障,进行修理,所用的时间是 小时;
(3)![]() 出发后 小时与
出发后 小时与![]() 相遇;
相遇;
(4)求![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.
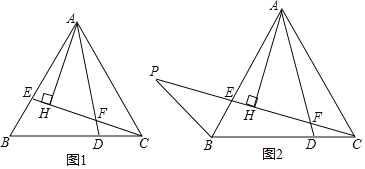
(1)求∠AFE的度数;
(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;
(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=![]() CP,求
CP,求![]() 的值.
的值.
(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)
查看答案和解析>>
科目:初中数学 来源: 题型:
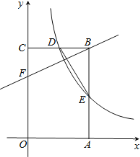
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,双曲线
,双曲线![]() ,的图象经过
,的图象经过![]() 上的点
上的点![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若若
,若若![]() 是
是![]() 的中点﹒
的中点﹒
(1)求![]() 点的坐标;
点的坐标;
(2)点![]() 是
是![]() 边上一点,若
边上一点,若![]() 和
和![]() 相似,求
相似,求![]() 的解析式;
的解析式;
(3)若点![]() 也在此反比例函数的图象上(其中
也在此反比例函数的图象上(其中![]() ),过
),过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,若线段
,若线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() ,设
,设![]() 点的纵坐标为
点的纵坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com