
【题目】如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.
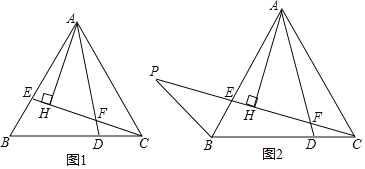
(1)求∠AFE的度数;
(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;
(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=![]() CP,求
CP,求![]() 的值.
的值.
(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)
【答案】(1)∠AFE=60°;(2)见解析;(3)![]()
【解析】
(1)通过证明![]() 得到对应角相等,等量代换推导出
得到对应角相等,等量代换推导出![]() ;
;
(2)由(1)得到![]() ,
,![]() 则在
则在![]() 中利用30°所对的直角边等于斜边的一半,等量代换可得;
中利用30°所对的直角边等于斜边的一半,等量代换可得;
(3)通过在PF上取一点K使得KF=AF,作辅助线证明![]() 和
和![]() 全等,利用对应边相等,等量代换得到比值.(通过将
全等,利用对应边相等,等量代换得到比值.(通过将![]() 顺时针旋转60°也是一种思路.)
顺时针旋转60°也是一种思路.)
(1)解:如图1中.

∵![]() 为等边三角形,
为等边三角形,
∴AC=BC,∠BAC=∠ABC=∠ACB=60°,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() (SAS),
(SAS),
∴∠BCE=∠DAC,
∵∠BCE+∠ACE=60°,
∴∠DAC+∠ACE=60°,
∴∠AFE=60°.
(2)证明:如图1中,∵AH⊥EC,
∴∠AHF=90°,
在Rt△AFH中,∵∠AFH=60°,
∴∠FAH=30°,
∴AF=2FH,
∵![]() ,
,
∴EC=AD,
∵AD=AF+DF=2FH+DF,
∴2FH+DF=EC.
(3)解:在PF上取一点K使得KF=AF,连接AK、BK,
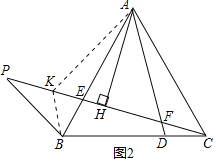
∵∠AFK=60°,AF=KF,
∴△AFK为等边三角形,
∴∠KAF=60°,
∴∠KAB=∠FAC,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() (SAS),
(SAS),![]()
∴∠AKB=∠AFC=120°,
∴∠BKE=120°﹣60°=60°,
∵∠BPC=30°,
∴∠PBK=30°,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴ .
.


科目:初中数学 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
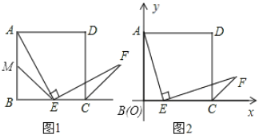
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 ![]() +
+ ![]() =2的解为正数,且不等式组
=2的解为正数,且不等式组 ![]() 无解的概率是________.
无解的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D

(1)求证:∠CAD =∠CAB(3分)
(2)已知抛物线![]() 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=![]() .
.
① 求抛物线的解析式(3分)
② 判断抛物线的顶点E是否在直线CD上,并说明理由(3分);
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由(3分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
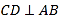
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装每天可售出20件![]() 为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利
为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利![]() 经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
![]() 如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
![]() 每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com