
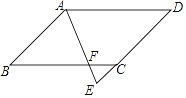
【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场花9万元从厂家购买A型和B型两种型号的电视机共50台,其中A型电视机的进价为每台1500元,B型电视机的进价为每台2500元.
(1)求该商场购买A型和B型电视机各多少台?
(2)若商场A型电视机的售价为每台1700元,B型电视机的售价为每台2800元,不考虑其他因素,那么销售完这50台电视机该商场可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
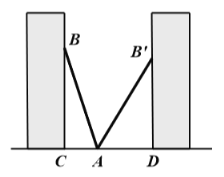
【题目】如图,小巷左右两侧是竖直的墙,一架梯子![]() 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离![]() 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离![]() 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离![]() 为2米,求小巷的宽度
为2米,求小巷的宽度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
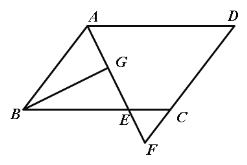
【题目】如图,在![]() ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=![]() ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.
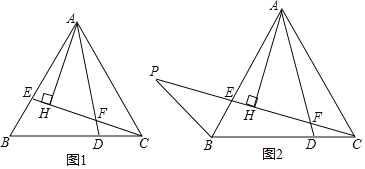
(1)求∠AFE的度数;
(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;
(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=![]() CP,求
CP,求![]() 的值.
的值.
(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com