
【题目】如图![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() 与
与![]() 时间的关系,根据图象回答下列问题:
时间的关系,根据图象回答下列问题:
(1)![]() 出发时与
出发时与![]() 相距 千米;
相距 千米;
(2)走了一段路后,![]() 自行车发生故障,进行修理,所用的时间是 小时;
自行车发生故障,进行修理,所用的时间是 小时;
(3)![]() 出发后 小时与
出发后 小时与![]() 相遇;
相遇;
(4)求![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
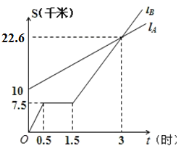
【答案】(1)10;(2)1;(3)3 ;(4)![]() .
.
【解析】
(1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5﹣0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)S和t的函数关系是一次函数,设函数是为S=kt+b,过(0,10)和(3,22.6),从而可求出关系式.
解:(1)由图形可得B出发时与A相距10千米;
故答案为:1
(2)在图中发现0.5至1.5小时,自行车没有行走,
故可得出修理所用的时间为1小时.
故答案为:1
(3)图中两直线的交点是B与A相遇的时刻,
即出发3小时后与A相遇.
故答案为:3
(4)设函数是为S=kt+b,且过(0,10)和(3,22.6),
则![]()
解得:![]()
故S与时间t的函数关系式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某校九年级(8)课外活动设置了如图所示的翻牌游戏,每次抽奖翻开一个数字,考虑“第一个人中奖排球”的机会.
正面
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
反面
排球 | 钢笔 | 图书 |
铅笔 | 空门 | 书包 |
球拍 | 小刀 | 篮球 |
(1)如果用实验进行估计,但制作翻奖牌没有材料,那么你有什么简便的模拟实验方法?
(2)如果不做实验,你能估计“第一个人中奖排球”的机会是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把能被13整除的数称为“自觉数”,已知一个整数,把其个位数字去掉,再从余下的数中加上个位数的4倍如果和是13的倍数,则原数为“自觉数”,如果数字仍然太大不能直接观察出来就重复此过程.如416:41+4×6=65,65÷13=5,所以416是自觉数;又如25281:2528+4×1=2532,253+4×2=261,26+4×1=30,因为30不能被13整除,所以25281不是“自觉数”.
(1)判断27365是否为自觉数 (填“是”或者“否”).
(2)一个四位数n=![]() ,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
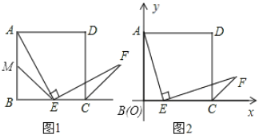
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 ![]() +
+ ![]() =2的解为正数,且不等式组
=2的解为正数,且不等式组 ![]() 无解的概率是________.
无解的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D

(1)求证:∠CAD =∠CAB(3分)
(2)已知抛物线![]() 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=![]() .
.
① 求抛物线的解析式(3分)
② 判断抛物线的顶点E是否在直线CD上,并说明理由(3分);
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由(3分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com