
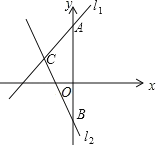
【题目】如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1相交于C(﹣3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式;
(2)求△ABC的面积.
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】我们把能被13整除的数称为“自觉数”,已知一个整数,把其个位数字去掉,再从余下的数中加上个位数的4倍如果和是13的倍数,则原数为“自觉数”,如果数字仍然太大不能直接观察出来就重复此过程.如416:41+4×6=65,65÷13=5,所以416是自觉数;又如25281:2528+4×1=2532,253+4×2=261,26+4×1=30,因为30不能被13整除,所以25281不是“自觉数”.
(1)判断27365是否为自觉数 (填“是”或者“否”).
(2)一个四位数n=![]() ,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
,规定F(n)=|a+d﹣b×c|,如:F(2019)=|2+9﹣0×1|=11,若四位数n能被65整除,且该四位数的千位数字和十位数字相同,其中1≤a≤4.求出所有满足条件的四位数n中,F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 ![]() +
+ ![]() =2的解为正数,且不等式组
=2的解为正数,且不等式组 ![]() 无解的概率是________.
无解的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D

(1)求证:∠CAD =∠CAB(3分)
(2)已知抛物线![]() 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=![]() .
.
① 求抛物线的解析式(3分)
② 判断抛物线的顶点E是否在直线CD上,并说明理由(3分);
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由(3分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
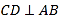
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
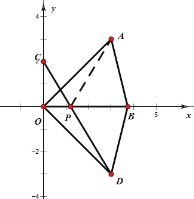
【题目】如图,A(3,3)、C(0,2),点B(b,0)是x轴正半轴上一动点,点D是点A关于x轴的对称点.
(1)写出点D的坐标并用b表示四边形AODB的面积S;
(2)连结CD交x轴于P,试求AP与CP的和;
(3)在点B从左向右移动过程中,点B处于哪些位置时△OBD是特殊的三角形?写出点B的坐标并分别说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com