
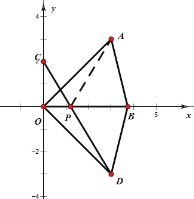
【题目】如图,A(3,3)、C(0,2),点B(b,0)是x轴正半轴上一动点,点D是点A关于x轴的对称点.
(1)写出点D的坐标并用b表示四边形AODB的面积S;
(2)连结CD交x轴于P,试求AP与CP的和;
(3)在点B从左向右移动过程中,点B处于哪些位置时△OBD是特殊的三角形?写出点B的坐标并分别说明理由.
【答案】(1)![]() ,S=3b;(2)AP+CP=
,S=3b;(2)AP+CP=![]() ;(3)当点B处于(3,0)和(6,0)时,△OBD是特殊的三角形,理由见解析
;(3)当点B处于(3,0)和(6,0)时,△OBD是特殊的三角形,理由见解析
【解析】
(1)根据两点关于x轴对称的特征即可确定点D的坐标,再根据四边形AODB的面积等于2S△AOB求解即可;
(2)根据“两点之间线段最短”进行求解即可;
(3)依据等腰三角形和等腰直角三角形的定义结合已知条件进行判断即可.
(1)∵点D是点A关于x轴的对称点
∴D(3,-3)
由已知可得△OBD和△AOB关于x轴对称
∴S= 2S△AOB=![]() =3b.
=3b.
(2)如图,
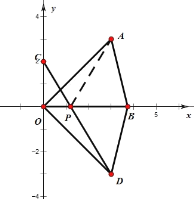
由已知和(1)可得,AP=PD
又CD=![]() =
=![]()
∴AP+CP=CD=![]() ;
;
(3)当点B处于(3,0),(![]() ,0)和(6,0)时,△OBD是特殊的三角形.理由如下:
,0)和(6,0)时,△OBD是特殊的三角形.理由如下:
∵D(3,-3)
∴∠DOB=45°
①当 B处于(3,0)时,△OBD是等腰直角三角形,且∠OBD=90°;
②当 B处于(6,0)时,△OBD是等腰直角三角形,且∠ODB=90°;
③当 B处于(![]() ,0)时,△OBD是等腰三角形,且OD=OB;
,0)时,△OBD是等腰三角形,且OD=OB;


科目:初中数学 来源: 题型:
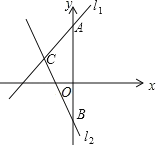
【题目】如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1相交于C(﹣3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
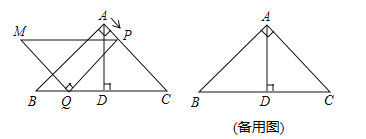
【题目】(2016吉林省)如图,在等腰直角三角形ABC中,∠BAC=90°,AC=![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过最高点(2,5)和点(0,4).
(1)试确定此二次函数的解析式;
(2)请你用图象法判断方程-![]() x2+x+1=0的根的情况.(画出简图)
x2+x+1=0的根的情况.(画出简图)
查看答案和解析>>
科目:初中数学 来源: 题型:
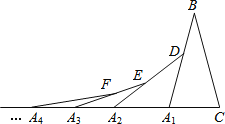
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.(![]() )n75°B.(
)n75°B.(![]() )n﹣165°
)n﹣165°
C.(![]() )n﹣175°D.(
)n﹣175°D.(![]() )n85°
)n85°
查看答案和解析>>
科目:初中数学 来源: 题型:
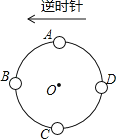
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
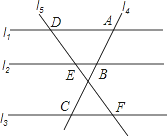
【题目】如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com