
【题目】已知二次函数的图象经过最高点(2,5)和点(0,4).
(1)试确定此二次函数的解析式;
(2)请你用图象法判断方程-![]() x2+x+1=0的根的情况.(画出简图)
x2+x+1=0的根的情况.(画出简图)
【答案】(1)y=-![]() x2+x+4(2)方程-
x2+x+4(2)方程-![]() x2+x+1=0由两个不相等的实数根,图见解析.
x2+x+1=0由两个不相等的实数根,图见解析.
【解析】
(1)二次函数最高点也是函数的顶点为(2,5),可设函数的表达式为y=a(x-2)2+5,把(0,4)代入上式,即可求解;
(2)原问题转化为-![]() x2+x+1=0根的情况,函数值为3的点由2个,因此方程-
x2+x+1=0根的情况,函数值为3的点由2个,因此方程-![]() x2+x+1=0由两个不相等的实数根.
x2+x+1=0由两个不相等的实数根.
(1)∵二次函数最高点也是函数的顶点(2,5),
∴函数的表达式为y=a(x-2)2+5,
把(0,4)代入上式,解得:a=-![]() ,
,
∴二次函数的解析式为:y=-![]() x2+x+4;
x2+x+4;
(2)原方程变形为:-![]() x2+x+4=3,
x2+x+4=3,
∴上述问题转化为-![]() x2+x+1=0根的情况,
x2+x+1=0根的情况,
∴函数值为3的点由2个,
则方程-![]() x2+x+1=0由两个不相等的实数根.
x2+x+1=0由两个不相等的实数根.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
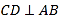
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装每天可售出20件![]() 为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利
为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利![]() 经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
![]() 如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
![]() 每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时开始攀登一座900 m高的山,第一组的攀登速度是第二组的1.2倍,他们比第二组早30 min到达顶峰.
(1)求这两个小组的攀登速度各是多少?
(2)如果山高为a m,第一组的攀登速度是第二组的b倍,并比第二组早t min到达顶峰,则两个小组的攀登速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
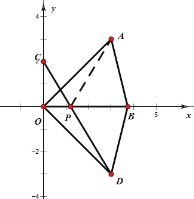
【题目】如图,A(3,3)、C(0,2),点B(b,0)是x轴正半轴上一动点,点D是点A关于x轴的对称点.
(1)写出点D的坐标并用b表示四边形AODB的面积S;
(2)连结CD交x轴于P,试求AP与CP的和;
(3)在点B从左向右移动过程中,点B处于哪些位置时△OBD是特殊的三角形?写出点B的坐标并分别说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
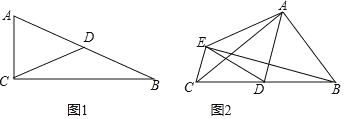
灵活应用:如图2,△ABC中,∠BAC=90°,AB=3, AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE, CE.
(1)求AD的长;
(2)判断△BCE的形状;
(3)求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
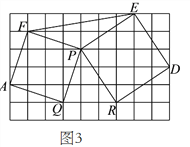
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com