
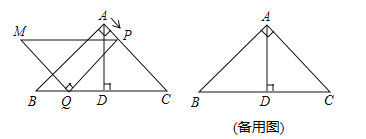
【题目】(2016吉林省)如图,在等腰直角三角形ABC中,∠BAC=90°,AC=![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】(1)4;(2)![]() ;(3)
;(3)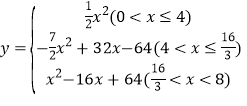 .
.
【解析】试题分析:(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,由此即可解决问题.
(2)如图1中,当点M落在AD上时,作PE⊥QC于E,先证明DQ=QE=EC,由PE∥AD,得![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当![]() <x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
<x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
试题解析:解:(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,AP=CP=![]() ,所以x=
,所以x=![]() =4.故答案为:4.
=4.故答案为:4.
(2)如图1中,当点M落在AD上时,作PE⊥QC于E.

∵△MQP,△PQE,△PEC都是等腰直角三角形,MQ=PQ=PC,∴DQ=QE=EC,∵PE∥AD,∴![]() =
=![]() ,∵AC=
,∵AC=![]() ,∴PA=
,∴PA=![]() ,∴x=
,∴x=![]() ÷
÷![]() =
=![]() .故答案为:
.故答案为:![]() .
.
(3)①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,
∵AP=![]() x,∴EF=PE=x,∴y=S△PEF=
x,∴EF=PE=x,∴y=S△PEF=![]() PEEF=
PEEF=![]() .
.
②当4<x≤![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.

∵PQ=PC=![]() ,∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,∴y=S△PMQ﹣S△MEG=
,∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,∴y=S△PMQ﹣S△MEG=![]() =
=![]() .
.

③当![]() <x<8时,如图4中,则重合部分为△PMQ,∴y=S△PMQ=
<x<8时,如图4中,则重合部分为△PMQ,∴y=S△PMQ=![]() =
=![]() =
=![]() .
.
综上所述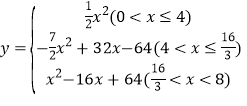 .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】图①②③是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.

(1)图①中△MON的面积=________;
(2)在图②③中以格点为顶点画出一个正方形ABCD,使正方形ABCD的面积等于(1)中△MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD的面积没有剩余(在图②、图③中画出的图形不能是全等形)
查看答案和解析>>
科目:初中数学 来源: 题型:
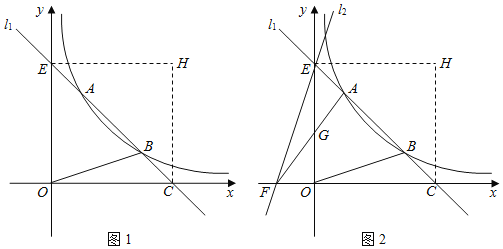
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?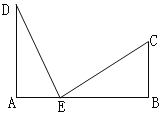
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式x3﹣3xy2﹣3的常数项是a,次数是b.则a= ,b= ;
并将这两数在如图所示数轴上所对应的点A、B表示出来;
![]()
操作探究:
操作一:
(1)折叠纸面,使A表示的点与B表示的点重合,则5表示的点与__ ___表示的点重合;
操作二: (2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①![]() 表示的点与数_____表示的点重合;
表示的点与数_____表示的点重合;
②若数轴上C、D两点之间距离为9,(C在D的左侧),且C、D两点经折叠后重合,求C、D两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定(a,b)※(c,d)=bc-ad
例如:(1,2)※(3,4)=2×3-1×4=2
根据上述规定解决下列问题:
(1)有理数对(4,-3)※(3,-2)=_______
(2)若有理数对(-3,2x-1)※(1,x+1)=7,则x=______
(3)当满足等式(-3,2x-1)※(k,x+k)=5+2k的x是非零整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C都在直线l上,AE⊥AB且AE=AB,BC⊥CD且BC=CD,三点E,B,D到直线l的距离分别是6,3,4,计算图中由线段AB,BC,CD,DE,EA所围成的图形的面积是( )
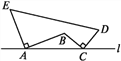
A. 50 B. 62 C. 65 D. 68
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com