
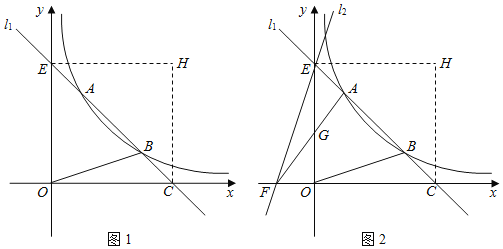
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
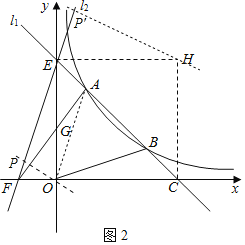
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)待定系数法求一次函数解析式和反比例函数解析式,将已知点坐标代入并解方程(组)即可;
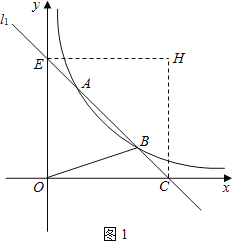
(2)先求出直线l1与坐标轴的交点坐标,可得:△COE是等腰直角三角形,再由翻折可得:OCHE是正方形.即可求出H的坐标;
(3)①先待定系数法求直线AO解析式为y=3x,再由△AEG的面积与△OFG的面积相等可得:EF∥AO,即可求直线l2的解析式;
②存在,由S△PBC=S△OBC可知:点P在经过点O或H平行于直线l1:y=-x+4的直线上,易求得点P的坐标为P(-1,1)或P(1,7).
解:(1)将![]() 、点
、点![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() 双曲线的解析式为:
双曲线的解析式为:![]() .
.
(2)如图1中,
在![]() 中,令
中,令![]() ,得:
,得:![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,
由翻折得:![]()
![]() ,
,![]()
![]() 是正方形.
是正方形.
![]() .
.
(3)如图2,连接![]() ,
,
①![]() 、
、![]() .设直线
.设直线![]() 解析式为
解析式为![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
![]()
![]()
![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
②存在,点![]() 坐标为:
坐标为:![]() 或
或![]() .
.
解方程组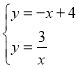 得:
得:![]() ,
,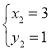 ;
;
![]() ;
;
![]() ,
,
![]() 点
点![]() 在经过点
在经过点![]() 或
或![]() 平行于直线
平行于直线![]() 的直线上,
的直线上,
易得:![]() 或
或![]()
分别解方程组![]() 或
或![]() 得:
得:![]() 或
或![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上,修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的甬道,设甬道的宽为a米.
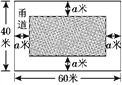 ①
①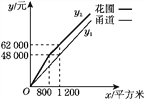 ②
②
(1)用含a的式子表示花圃的面积;
(2)如果甬道所占面积是整个长方形空地面积的![]() ,求此时甬道的宽;
,求此时甬道的宽;
(3)已知某园林公司修建甬道、花圃的造价y1(元)、y2(元)与修建面积x(平方米)之间的函数关系如图②所示.如果学校决定由该公司承建此项目,并要求修建的甬道宽不少于2米且不超过10米,那么甬道的宽为多少米时,修建的甬道和花圃的总造价最低?最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的部分函数图象为折线OA-AB-BC,如图所示.
(1)求工人一天加工零件不超过20个时每个零件的加工费.
(2)求40≤![]() ≤60时y与x的函数关系式.
≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元.在这两天中,小王第一天加工零件不足20个,求小王第一天加工的零件个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:

(1)3.8秒时,哪位同学处于领先位置?
(2)在这次赛跑中,哪位同学先到达终点?比另一个同学早多少时间到达?约几秒后哪位同学被哪位同学追上?
(3)甲同学所走的路程S(米)与时间t(秒)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
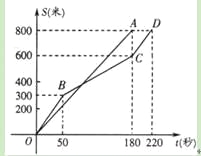
A. 小莹的速度随时间的增大而增大B. 小梅的平均速度比小莹的平均速度大
C. 在起跑后180秒时,两人相遇D. 在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
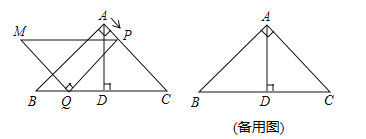
【题目】(2016吉林省)如图,在等腰直角三角形ABC中,∠BAC=90°,AC=![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
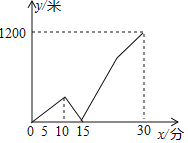
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com