搜索
【题目】甲、乙两同学在一次百米赛跑中，路程S（米）与时间t（秒）之间的关系如图所示．根据图象回答下列问题：
（1）3.8秒时，哪位同学处于领先位置？
（2）在这次赛跑中，哪位同学先到达终点？比另一个同学早多少时间到达？约几秒后哪位同学被哪位同学追上？
（3）甲同学所走的路程S（米）与时间t（秒）之间的函数关系式．
参考答案：
【答案】（1）甲；（2）乙，比甲提早0.5秒，
秒后甲同学被乙同学追上；（3）S=8t．
【解析】
试题分析：（1）由图象得出3.8秒时甲处于领先位置；
（2）由图象得出乙先到达终点，且早到0.5秒，列出两个解析式得出两直线的交点解答；
（3）利用待定系数法得出甲的解析式即可．
试题解析：（1）由图象可得3.8秒时，甲处于领先位置；
（2）由图象可得：乙先到达终点，且乙比甲早到12.5﹣12=0.5秒；
设甲的解析式为S=at，把（12.5，100）代入S=at中，可得：100=12.5a，解得：a=8，所以甲的解析式为S=8t，设乙的解析式为S=kt+b，把（6，30）和（12，100）代入解析式S=kt+b，可得：
，解得：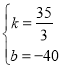
．所以解析式为：
，联立两个方程得：
，解得：t=．
所以秒后甲同学被乙同学追上；
（3）设甲的解析式为S=at，把（12.5，100）代入S=at中，可得：100=12.5a，解得：a=8．
所以甲的解析式为S=8t．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．设甲、乙两车间各自加工大米数量y（吨）与甲车间加工时间s（天）之间的关系如图（1）所示；未加工大米w（吨）与甲加工时间x（天）之间的关系如图（2）所示，请结合图象回答下列问题：
（1）甲车间每天加工大米 吨，a= ．
（2）求乙车间维修设备后，乙车间加工大米数量y（吨）与x（天）之间函数关系式．
（3）若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某一食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
这批样品的平均质量比标准质量多还是少？多或少几克，若标准质量为450克，则抽样检测的总质量是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间存在一次函数关系．从温度计的刻度上可以看出，摄氏温度x（℃）与华氏温度y（℉）有如下的对应关系：
x（℃）
…
－10
0
10
20
30
…
y（℉）
…
14
32
50
68
86
…
（1）试确定y与x之间的函数关系。
（2）某天，滨海的最高气温是25℃，澳大利亚悉尼的最高气温80℉，这一天哪个地区的最高气温较高？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：
例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8-6）=20（元）．
请根据上表的内容解答下列问题：
（1）若某户居民2月份用水5立方米，则应收水费多少元？
（2）若某户居民3月份交水费36元，则用水量为多少立方米？
（3）若某户居民4月份用水a立方米（其中6＜a＜10），请用含a的代数式表示应收水费．
（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水x立方米，请用含x的代数式表示该户居民5、6两个月共交水费多少元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是一次函数y=kx+b的图象．
（1）求这个一次函数的解析式？
（2）试判断点P（1，-1）是否在这个一次函数的图象上？
（3）求原点O到直线AB的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】进入冬季，我市空气质量下降，多次出现雾霾天气．商场根据市民健康需要，代理销售一种防尘口罩，进货价为20元/包，经市场销售发现：销售单价为30元/包时，每周可售出200包，每涨价1元，就少售出5包．若供货厂家规定市场价不得低于30元/包，且商场每周完成不少于150包的销售任务．
（1）试确定周销售量y（包）与售价x（元/包）之间的函数关系式；
（2）试确定商场每周销售这种防尘口罩所获得的利润w（元）与售价x（元/包）之间的函数关系式，并直接写出售价x的范围；
（3）当售价x（元/包）定为多少元时，商场每周销售这种防尘口罩所获得的利润w（元）最大？最大利润是多少？
相关试题
