
����Ŀ��ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺���������Ͷ���г��������������г����������۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3���������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ���ÿ����ܳɱ���ÿ���ijɱ���ÿ�����������
���𰸡���1��y=![]() +800x��27500��50��x��100���� ��2�����۵���Ϊ80Ԫʱ��ÿ�������������������������4500Ԫ����3�����۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮����
+800x��27500��50��x��100���� ��2�����۵���Ϊ80Ԫʱ��ÿ�������������������������4500Ԫ����3�����۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮����
��������
�����������1������������=���ۼ�-�ɱ��������������г����̣���2������1���еĶ��κ�������ʽת��Ϊ����ʽ���������ö��κ���ͼ������ʽ��н����3����y=4000���뺯������ʽ�������Ӧ��xֵ��Ȼ������ÿ����ܳɱ�������7000Ԫ���г�����x�IJ���ʽ50��-5x+550����7000��ͨ���ⲻ��ʽ����x��ȡֵ��Χ��
�����������1��y=��x��50��[50+5��100��x��]=��x��50������5x+550��=![]() +800x��27500����y=
+800x��27500����y=![]() +800x��27500��50��x��100����
+800x��27500��50��x��100����
��2��y=![]() +800x��27500=
+800x��27500=![]() +4500����a=��5��0���������߿�����������50��x��100���Գ�����ֱ��x=80������x=80ʱ��
+4500����a=��5��0���������߿�����������50��x��100���Գ�����ֱ��x=80������x=80ʱ��![]() =4500��
=4500��
��3����y=4000ʱ��![]() +4500=4000�����
+4500=4000�����![]() ��
��![]() ������70��x��90ʱ��ÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����50����5x+550����7000�����x��82����82��x��90����50��x��100�������۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮����
������70��x��90ʱ��ÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����50����5x+550����7000�����x��82����82��x��90����50��x��100�������۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ��һ�ΰ��������У�·��S���ף���ʱ��t���룩֮��Ĺ�ϵ��ͼ��ʾ������ͼ��ش��������⣺

��1��3.8��ʱ����λͬѧ��������λ�ã�
��2������������У���λͬѧ�ȵ����յ㣿����һ��ͬѧ�����ʱ�䵽�Լ�������λͬѧ����λͬѧ�ϣ�
��3����ͬѧ���ߵ�·��S���ף���ʱ��t���룩֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������2��1ǧ��ѧУ�μӳ��������ᣬ��ѧУʱ�����ݳ��������ڼ��У���ʱ�������Ὺʼ����42���ӣ��������������ٲ��лؼң��ڼ��õ�������1���ӣ�Ȼ���������������г�����ѧУ����֪���������г���ѧУ������ѧУ���е�����ʱ��20���ӣ��������г����ٶ��Dz����ٶȵ�3����
��1���������е��ٶȣ���λ����/�֣��Ƕ��٣�
��2�������ܷ��������Ὺʼǰ�ϵ�ѧУ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C������ƽ��ͼ��C����A���ı�ƫ��50������B����A���ı�ƫ��80������C����B���ı�ƫ��50������B����A��C�������ӽ���ABC�Ƕ��ٶȣ���C����A��B�������ӽ���ACB�أ�
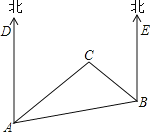
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ����
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ����
С���������13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-������![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ���������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ������x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���뾶Ϊ1��Բ����Ƥ�м���һ��Բ�Ľ�Ϊ90�������BAC��
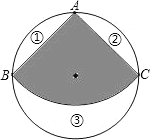
��1���������������
��2����������BACΧ��һ��Բ�IJ��棬���Բ�ĵ���ֱ���Ƕ��٣��ܷ���������Ϣ��м���һ��Բ����Բ�ĵ��棿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г���շѱ��ǣ���10Ԫ���ɳ�3ǧ����3ǧ����5ǧ����ÿǧ��1��3Ԫ������5ǧ����ÿǧ��2��4Ԫ��
��1����ij�˳�����![]() ��
��![]() ��ǧ��·�̣�����Ӧ֧���ķ����Ƕ��٣�
��ǧ��·�̣�����Ӧ֧���ķ����Ƕ��٣�
��2����ij�˳�����·��Ϊ6ǧ������ô��Ӧ֧���ķ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ������������й��������й�����ת�͵ĺ��٣�ij��˾���������һ��ɱ�Ϊ40Ԫ�Ŀɿ��±�����Ͷ���г����������ۣ��������鷢�ָò�Ʒÿ���������y�����������۵���x��Ԫ������һ�κ�����ϵ��y=��10x+1200��
��1��������S��Ԫ�������۵���x��Ԫ��֮��Ĺ�ϵʽ��
��2�������۵��۶�Ϊ����ʱ���ù�˾ÿ���ȡ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com