
【题目】某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的部分函数图象为折线OA-AB-BC,如图所示.
(1)求工人一天加工零件不超过20个时每个零件的加工费.
(2)求40≤![]() ≤60时y与x的函数关系式.
≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元.在这两天中,小王第一天加工零件不足20个,求小王第一天加工的零件个数.

【答案】(1)3元;(2)![]() .(3)小王第一天加工10个零件
.(3)小王第一天加工10个零件
【解析】解:(1)由图象可知,当0≤x≤20时,每个零件的加工费为60÷20=3元,
即工人一天加工零件不超过20个时,每个零件的加工费为3元。
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,
将B(40,140),C(60,240)代入,得
![]() ,解得
,解得![]() 。
。
∴y与x的函数关系式为y=5x-60。
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),
∵ 小王第一天加工的零件不足20个,小王两天一共加工了60个零件。
∴小王第二天加工的零件不足60个,超过40个。
由(2)知,第二天加工零件的加工费为5(60-a)-60。
∴5(60-a)-60=220-3a,解得,a =10。
∴小王第一天加工零件10个。
(1)当0≤x≤20时,由图象得出每个零件的加工费为60÷20=3元。
(2)当40≤x≤60时,设y与x的函数关系式为y=kx+b,将(20,60),(40,140)代入,列方程组求k、b的值即可。
(3)设小王第一天加工零件的个数为a,则第二天加工零件的个数为(60-a),由(2)知,第二天加工零件的加工费为5(60-a)-60,因此列方程5(60-a)-60=220-3a求解。


科目:初中数学 来源: 题型:
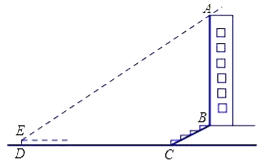
【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
【答案】33.3.
【解析】
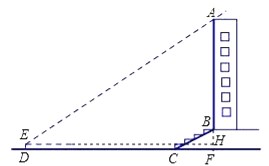
试题分析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
试题解析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,![]() =i=1:
=i=1:![]() ,∴设BF=k,则CF=
,∴设BF=k,则CF=![]() k,BC=2k.
k,BC=2k.
又∵BC=12,∴k=6,∴BF=6,CF=![]() .∵DF=DC+CF,∴DF=40+
.∵DF=DC+CF,∴DF=40+![]() .∵在Rt△AEH中,tan∠AEH=
.∵在Rt△AEH中,tan∠AEH=![]() ,∴AH=tan37°×(40+
,∴AH=tan37°×(40+![]() )≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.
)≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.
答:大楼AB的高度约为33.3米.
考点:1.解直角三角形的应用-仰角俯角问题;2.解直角三角形的应用-坡度坡角问题.
【题型】解答题
【结束】
24
【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
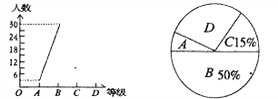
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:

(1)请补全统计图;
(2)在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是________度;
(3)该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x,y满足y<![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成不完整的统计表,请根据图表中的信息解答下列问题.
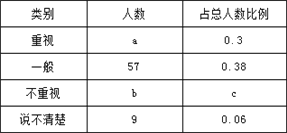
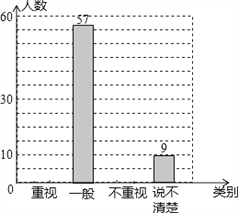
(1)样本容量为 ,表格中c的值为 ,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为 ;
(3)根据上面的数据统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com