
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

【答案】(1)DF=EF+BE.理由见解析;(2)CF=4.
【解析】(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AEF≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)根据旋转的性质的AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,根据勾股定理有FG2=FC2+CG2=BE2+FC2;关键全等三角形的性质得到FG=EF,利用勾股定理可得CF.
解:(1)DF=EF+BE.理由:如图1所示,

∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠ABE=90°,∴点C、D、G在一条直线上,∴EB=DG,AE=AG,∠EAB=∠GAD,
∵∠BAG+∠GAD=90°,∴∠EAG=∠BAD=90°,
∵∠EAF=45°,∴∠FAG=∠EAG﹣∠EAF=90°﹣45°=45°,∴∠EAF=∠GAF,
在△EAF和△GAF中,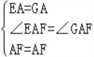 ,∴△EAF≌△GAF,∴EF=FG,∵FD=FG+DG,∴DF=EF+BE;
,∴△EAF≌△GAF,∴EF=FG,∵FD=FG+DG,∴DF=EF+BE;
(2)∵∠BAC=90°,AB=AC,∴将△ABE绕点A顺时针旋转90°得△ACG,连接FG,如图2,
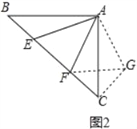
∴AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,而∠EAG=90°,∴∠GAF=90°﹣45°,
在△AGF与△AEF中,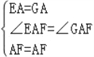 ,∴△AEF≌△AGF,∴EF=FG,
,∴△AEF≌△AGF,∴EF=FG,
∴CF2=EF2﹣BE2=52﹣32=16,∴CF=4.
“点睛”本题考查了全等三角形的性质和判定,勾股定理,正方形的性质的应用,正确的作出辅助线构造全等三角形是解题的关键,此题是一道综合题,难度较大,题目所给例题的思路,为解决此题做了较好的铺垫.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(4,0),经过点A点B抛物线y=x+bx+c与y轴交于点C.
(1)求抛物线的关系式.
(2)△ABC的外接圆与y轴交于点D,在抛物线上是否存在点M使S△MBC=S△DBC,若存在,请求出点M的坐标.
(3)点P是直线y=-x上一个动点,连接PB,PC,当PB+PC+PO最小时,求点P的坐标及其最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=![]() (k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
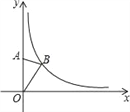
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定一个四边形是菱形的条件是( )
A. 对角线互相平分且相等 B. 对角线互相垂直且相等
C. 对角线互相垂直且对角相等 D. 对角线互相垂直,且一条对角线平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各选项给出的是三角形中各边的长度的平方比,其中不是直角三角形的是( )
A. 1∶1∶2 B. 1∶3∶4 C. 9∶25∶36 D. 25∶144∶169
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2向右平移1个单位,再向上平移5个单位,则平移后的抛物线的解析式为( )
A.y=2(x+1)2+5
B.y=2(x+1)2﹣5
C.y=2(x﹣1)2﹣5
D.y=2(x﹣1)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子变形是因式分解的是【 】
A.x2-5x+6=x(x-5)+6 B.x2-5x+6=(x-2)(x-3)
C.(x-2)(x-3)=x2-5x+6 D.x2-5x+6=(x+2)(x+3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com